 This question has not perhaps been phrased in the best way. I would suggest the following
This question has not perhaps been phrased in the best way. I would suggest the following
EDIT.
If it is always possible to draw, through any point P:$(x,y)=(3-h,h)$, two distinct lines tangent to the cubic C:$y=x^3-9x^2-px+q$, find $p$ and $q$.
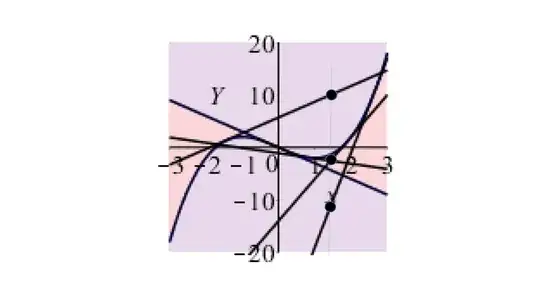
SOLUTION. Consider a cubic C with its inflexion point at the origin, $y= x^3+cx$, with tangent T through the origin $y=cx$. Then if $c\ge 0$ there always exists only one line tangent to $C$ through a given point P not on C. If $c<0$ there are two tangents through any point P located between C and T or on T. Through any other point there is only one tangent. Note that there is only one straight line from every point of which two tangents are always possible, and that is T itself. This is evident from inspection of this graph; an analytical proof is left to the reader.
In the question, the inflexion point is at $x=3$ and the tangent through the inflexion point is $$y=y(3)+y'(3)(x-3)=q+27-(p+27)x$$ and if this is to coincide with the line $y=3-x$ on which P always lies, then $p=-26$ and $q=-24$.
