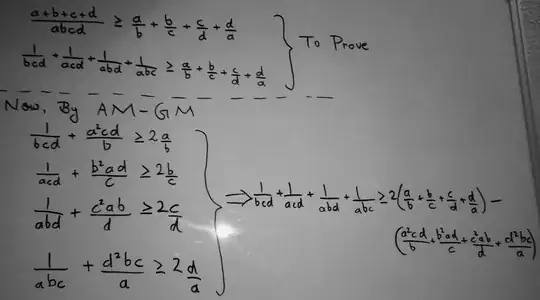8

$$\frac{4}{abcd}\geq\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}$$

Given: $a+b+c+d=4$ and $a$, $b$, $c$ abd $d$ are positives.

How to prove the above inequality using Arithmetic Geometric Mean Inequality?

I tried the following but, I am getting stuck after last step.

Solution

Michael Rozenberg
  • 203,855
Mrigank Shekhar Pathak
  • 1,024

1 Answers1

3

Let $\{a,b,c,d\}=\{x,y,z,t\}$, where $x\geq y\geq z\geq t$.

Hence, by Rearrengement and AM-GM we obtain: $$\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}=\frac{1}{abcd}(a^2cd+b^2da+c^2ab+d^2bc)=$$ $$=\frac{1}{abcd}(a\cdot acd+b\cdot bda+c\cdot cab+d\cdot dbc)\leq$$ $$\leq\frac{1}{abcd}(x\cdot xyz+y\cdot xyt+z\cdot xzt+t\cdot yzt)=$$ $$=\frac{1}{abcd}(x^2yz+y^2xt+z^2xt+t^2yz)=\frac{1}{abcd}(xy+zt)(xz+yt)\leq$$ $$\leq\frac{1}{abcd}\left(\frac{xy+zt+xz+yt}{2}\right)^2=$$ $$=\frac{1}{4abcd}\left((x+t)(y+z)\right)^2\leq\frac{1}{4abcd}\left(\frac{x+y+z+t}{2}\right)^4=\frac{4}{abcd}.$$ Done!

Michael Rozenberg
  • 203,855
  • 1
    I think this problem was designed by you because, the document in which I found it has your name attached beside the problem. Thank You for the solution. – Mrigank Shekhar Pathak Apr 14 '17 at 09:38
  • @Mrigank Shekhar Pathak Yes, you are right! It's my problem and my solution, but an idea with $x\geq y\geq z\geq t$ is not mine. – Michael Rozenberg Apr 14 '17 at 09:44
  • so, how you framed it initially. – Mrigank Shekhar Pathak Apr 14 '17 at 09:45
  • Homogenzing the ineq gets us $(a+b+c+d)^4\ge 64(a^2cd+b^2da+c^2ab+d^2bc)$ which exapands to $$\sum a^4+4\sum a^3b +12\sum a^2bc \ge 64(a^2cd+b^2da+c^2ab+d^2bc)$$ - no doubt it can be finished off with bunching and muirheading/ weighted AM-GM/ Schur ; but is there a better approach ? – rah4927 Apr 14 '17 at 09:56
  • @rah4927 You missed $6\sum\limits_{cyc}a^2b^2$. I think would be better if you check my solution. – Michael Rozenberg Apr 14 '17 at 10:22