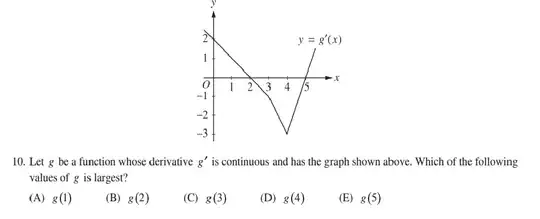
I answered this as g(5), and my justification was that at the first part of the drawing(until x = 4) $g^{'}$ is negative, so the function was decreasing. after $x=4$, $g^{'}$ is positive, so the function is increasing. but my answer was wrong, could anyone trace where is my wrong thought?
I have to answer the question in no more than 2.5 minutes.
Asked
Active
Viewed 1,452 times
1
Emptymind
- 2,217
-
1GRE Subject Test - Past Papers, Books, Advice – BCLC Apr 16 '17 at 19:33
1 Answers
1
You are confusing the slope in the plot of $g'$ with the sign of $g'$.
Since $g'$ is positive on $[0,2]$, $g$ is increasing there. Then $g'$ is negative on $[2,5]$ so it is decreasing there. So $g(2)$ is the maximum.
angryavian
- 93,534