6

Consider the integral:

$$ \int_0^{\pi/2}\sqrt{\sin t}e^{-x\sin^4 t} \, dt $$

I'm trying to use Laplace's method to find its leading asymptotic behavior as $x\rightarrow\infty$, but I'm running into problems because the maximum of $\phi(t)$ (i.e. $-\sin^{4}t$) is $0$ and occurs at $0$ (call this $c$). In my notes on the Laplace Method, it specifically demands that $f(c)$ (in this case $f(t)=\sqrt{\sin t}$) cannot equal zero--but it does. How do I get around this?

kjetil b halvorsen
  • 7,004
Alex
  • 889
  • 5
  • 12

2 Answers2

2

Plot integrand for few values of $x$:

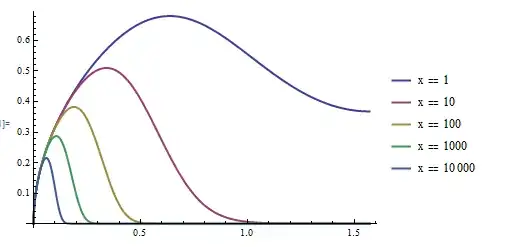
enter image description here

It is apparent that the maximum shifts closer to the origin as $x$ grows.

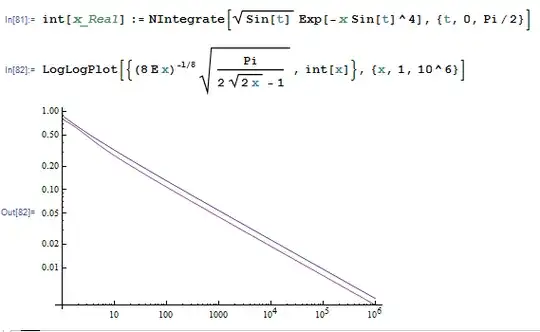
Let's rewrite the integrand as follows: $$ \int_0^{\pi/2} \sqrt{\sin(t)} \exp\left(-x \sin^4(t)\right) \mathrm{d}t = \int_0^{\pi/2} \exp\left(\frac{1}{2} \log(\sin(t))-x \sin^4(t)\right) \mathrm{d}t $$ The maximum of the integrand is determined by $$ 0 = \frac{\mathrm{d}}{\mathrm{d}t} \left(\frac{1}{2} \log(\sin(t))-x \sin^4(t)\right) = \cot(t) \left( \frac{1}{2} - 4 x \sin^4(t)\right) $$ that is at $t_\ast = \arcsin\left((8 x)^{-1/4}\right)$. Then using Laplace's method: $$ \int_0^{\pi/2} \sqrt{\sin(t)} \exp\left(-x \sin^4(t)\right) \mathrm{d}t \approx \int_{0}^{\pi/2} \exp\left(\phi(t_\ast) + \frac{1}{2} \phi^{\prime\prime}(t_\ast) (t-t_\ast)^2 \right) \mathrm{d}t = \exp\left(\phi(t_\ast)\right) \sqrt{\frac{2\pi}{-\phi^{\prime\prime}(t_\ast)}} $$ Easy algebra gives $\exp\left(\phi(t_\ast)\right) = (8 \mathrm{e} x)^{-1/8}$, $-\phi^{\prime\prime}(t_\ast) = 4 \sqrt{2 x} - 2$, giving $$ \int_0^{\pi/2} \sqrt{\sin(t)} \exp\left(-x \sin^4(t)\right) \mathrm{d}t \approx (8 \mathrm{e} x)^{-1/8} \sqrt{ \frac{\pi}{2 \sqrt{2 x} -1}} $$ enter image description here

Sasha
  • 71,686
1

The accepted answer is incorrect. Denote your integral by $I(x)$. Performing the change of integration variables from $t$ to $s$ via $t = \arcsin (s^{1/4} )$ gives $$ I(x) = \frac{1}{4}\int_0^1 {{\rm e}^{ - xs} \frac{{{\rm d}s}}{{s^{5/8} \sqrt {1 - s^{1/2} } }}} . $$ A straightforward application of Watson's lemma yields the asymptotic expansion $$ I(x) \sim \frac{1}{4}\frac{1}{{x^{3/8} }}\sum\limits_{n = 0}^\infty {\binom{n - 1/2}{n}\Gamma \bigg( {\frac{n}{2} + \frac{3}{8}} \bigg)\frac{1}{{x^{n/2} }}} , $$ as $x\to+\infty$. This result agrees with the leading-order asymptotics provided here.

Gary
  • 36,640