27

I'm trying to do limits in 3D and I'm wondering whether or not there are paths along which the limit of any function at any point can always be found. In my book it isn't clear whether this exists or not; neither is it clear how to choose a path if this does exist.

In the book they replace $y$ with $kx$ a lot but sometimes they replace $x$ and $y$ with $0$ separately and sometimes they use $x^2$.

I've seen some people have already asked similar questions but about specific formulas and I can't link that to my exact question.

Thanks for any help!

Rory McEwan
  • 579

4 Answers4

22

I know what you're asking, and the answer is "no" (caveat after reading the comments: There are paths that do conclude for you, most importantly so-called space-filling curves, but they are mostly of theoretical value, and rarely help in calculations). Checking different (simple) paths is not enough to show that a limit exists. It is good for two things, though:

  1. Finding a candidate limit. If you pick a path, and calculate the limit along that path, then you have a candidate for what the limit could be. Most limit calculations become easier once you have a concrete candidate to check.
  2. Showing that there is no limit. If two different paths create two different candidates, or if a single pay fails to give a limit, then there cannot be a single limit value at the given point.

The standard example is $$ f(x,y)=\cases{0&if $x=y=0$\\\frac{2x^2y}{x^4+y^2}&otherwise} $$for which every line through the origin says that the limit at the origin is $0$, while the parabola $y=x^2$ says that the limit is $1$. In general, there is no way of knowing that there isn't such a "different path". For instance, this example is not difficult to change into one where the path that gives $1$ is $y=x^{10}$ instead. How will you know in general that there isn't such a path hidden somewhere? That's impossible without proving the general limit in the first place.

Arthur
  • 204,511
  • I would add a concrete example of a function which doesn't have a limit but which does have a limit along path $\gamma$. The indicator function on $\gamma$, for example. – Patrick Stevens Mar 15 '17 at 07:17
  • 3
    I am not sure whether I misunderstood something, but I believe my answer shows that it is even sufficient to check a single path to prove that a limit exists. – Bananach Mar 15 '17 at 08:31
  • 2
    @Arthur: I agree with Bananach. The OP asks if there "are paths along which the limit of any function at any point can always be found" Your answer demonstrates that the obvious paths don't work, but Bananach's answer demonstrates that there are non-obvious paths which do work. – Jason DeVito - on hiatus Mar 15 '17 at 14:27
  • @Bananach You're right, I was too quick there. – Arthur Mar 15 '17 at 18:04
  • 1
    I think you can drop that "mostly" and change "rarely" to "never" in the caveat. While Bananach's trick is an excellent theoretic result, it is beyond impractical for any real-world calculation. – Paul Sinclair Mar 16 '17 at 00:23
18

Correct me if I'm wrong, but I believe existence of a limit may indeed be seen by only looking at a single path, if admittedly an odd path.

Let's say you want to know whether $f$ has a limit at $(0,0)\in\mathbb{R}^2$. Let $\gamma_1$ be a space-filling curve, i.e. a path whose image is the (entire!) square $[-1,1]^2$. Let $\gamma_n:=\gamma_1/n$, i.e. a path whose image is the square with side lengths $2/n$. Finally, let $\gamma$ be the concatenation of all those paths, with straight segments connecting the end of $\gamma_{n-1}$ with the start of $\gamma_n$. You can do all of this in such a way that $\gamma$ is defined on $[0,1]$ with $\gamma(1)=(0,0)$

Now if $f$ does have a limit at $(0,0)$, then $f\circ \gamma$ will have the same limit, as $\gamma$ after some while will live in the square $[-1/n,1/n]$ only. Conversely, if $f\circ \gamma$ has a limit $a$, then so does $f$ at $(0,0)$ since if there existed $x_n\to (0,0)$, $f(x_n)\not\to a$ then $(f\circ\gamma)(y_n)\not\to a$, where $y_n$ are chosen such that $\gamma(y_n)=x_n$ and $y_n\to 1$ (which is possible by surjectivity of each $\gamma_n$ onto a neighborhood of $(0,0)$.)

The practicability of this approach to verify limits by hand is of course limited, but we are just mathematicians after all.

Bananach
  • 8,332
  • 3
  • 32
  • 53
  • 4
    Assuming this works, note the curve passes through $(0,0)$; either you need to make a modification to avoid it, or you need to modify the conclusion to proving whether $f$ is continuous at $(0,0)$. –  Mar 15 '17 at 12:13
  • @Hurkyl My answer proves: "There exists a path such that for each function f defined on all the square, f is continuous at the origin if and only if f has a limit along this path" Do you agree with this and think it should be made more clear that this is what is being proved? – Bananach Mar 15 '17 at 12:59
  • 4
    Mathematicians can be the best trolls sometimes. – mercio Mar 15 '17 at 13:55
  • Is there any reason to think that, given a space-filling curve $\gamma$, one couldn't construct a function that specifically breaks this? – Glen O Mar 15 '17 at 15:45
  • 2
    To address Hurkyl's complaint without having to require continuity of $f$, you could have each $\gamma_n$ fill some shrinking annular region instead of the entire square. – Paul Sinclair Mar 15 '17 at 16:50
  • @GlenO - You cannot do so. If the limit along the curve exists, then for each $\epsilon$ there is a $\delta < 1 : t >\delta \implies |f(\gamma(t)) - L| <\epsilon$, But by the construction, $\gamma((\delta,1))$ completely fills a neighborhood of $(0,0)$, thus for any point (x,y) in that neighborhood $f(x,y) = f(\gamma(t))$ for some $t\in (\delta,1))$, so it is within $\epsilon$ of $L$. – Paul Sinclair Mar 15 '17 at 16:57
  • @PaulSinclair - I can see the reasoning of that argument, but allow me to pose the flipside argument. The space-filling curve is the limit of a sequence of approximants, $U_n(t)$. For any particular $n$, it is possible to construct a function $f_n(x,y)$ such that $f_n(U_n(t))$ has a limit but $f_n(x,y)$ does not have a limit. Why should this change in the limit as $n\to\infty$? – Glen O Mar 15 '17 at 17:23
  • I think what @Hurkyl says is that your technique cannot distinguish between the case where the limit exists but is unequal to $f(0,0)$ (removable discontinuity), and the case where the limit does not exist. Also, it is often the case that $f$ is not even defined in $(0,0)$ itself. So it seems you must "correct" the value in $(0,0)$ before you use your $\gamma$. – Jeppe Stig Nielsen Mar 15 '17 at 23:04
  • @GlenO - Because I've already demonstrated directly and succintly by the definition of the limit that if $\lim_{t\to 1}f\circ\gamma(t)$ exists, then $\lim_{(x,y)\to(0,0)}f(x,y)$ converges to the same value. If you can spot a flaw in my logic, or else complete your "this idea sorta-kinda hints that maybe if you hold your tongue just right it possibly could maybe lead to a counterexample" argument into a fully fleshed actual counter-example, then there is something to talk about. – Paul Sinclair Mar 15 '17 at 23:29
  • @PaulSinclair - the possible flaw in your argument is that it relies on a description, rather than direct mathematics. "The curve completely fills a neighbourhood" is a description. So let me provide an obvious construction of a function sequence satisfying my requirements for each step - the indicator function for $U_n(t)$ - that is, its value is 1 when $(x,y)=U_n(t)$ for some $t$ and its value is zero otherwise. Can you show that the indicator function $f_\infty(x,y)=1$, at least in the vicinity of $(0,0)$? – Glen O Mar 16 '17 at 02:53
  • 2
    @GlenO - Comments are not conducive to giving full proofs. Those particular details are obvious enough that anyone reasonably proficient should be able to see how to fill them. $\gamma$ consists of an infinite progression of space-filling curves for progessively smaller squares tied together. Any neighborhood of $1$ will contain an infinite number of them. It only takes one such such square to provide the needed neighborhood of $(0,0)$. – Paul Sinclair Mar 16 '17 at 03:44
  • As for your function, of course I can't. That function is a mixture of $0,1$, and undefined values. But it also has no bearing on this question, which is about the limit of a fixed function defined everywhere in a neighborhood of $(0,0)$ with respect to $(x,y)$ - not $n$. – Paul Sinclair Mar 16 '17 at 03:45
  • 1
    @Jeppe Stig Nielsen, the first comment of Paul Sinclair already says how to solve this. To be a bit more specific, for $\gamma_1$ you can use a space-filling curve that fills $[-1,1]^2 \setminus [-\frac12,\frac12]^2$. It's not hard to construct such a curve once you know how to construct a space-filling curve that fills $[-1,1]^2$. – Paul Mar 16 '17 at 11:02
  • @PaulSinclair - your argument is completely inadequate. If $f_\infty$ can be zero in some places, or undefined in some places, then I have demonstrated that the limit need not exist, as $\gamma$ is constructed recursively and thus there are points in the neighbourhood of $(0,0)$ that are either undefined or not sufficiently close to the supposed limit value. And the fact that the "squares" get smaller and smaller proves nothing. I can construct a spiral with $r=e^{-\theta}$ in polar, and it will contain an infinite number of spirals, but it doesn't work as a sufficient path for proof of limit. – Glen O Mar 17 '17 at 04:09
  • @GlenO - You have demonstrated that $\lim_{n\to \infty} f_n(x,y)$ for fixed $(x,y)$ may fail to exist (note: $n$, not $(x,y)$. But what you needed to show was that $\lim_{(x,y)\to (0,0)} f(x,y)$ fails to exist when $\lim_{t\to 1}f(\gamma(t))$ does exist, or vice versa (note: $(x, y)$ and $t$, not $n$). You have accomplished nothing towards that. And your supposed counter-example curve does not even begin to touch the argument I made. – Paul Sinclair Mar 17 '17 at 22:43
  • @PaulSinclair - my "counterargument" isn't a counterargument, it's an indication of a hole in your argument - a hole that may be easily filled (I actually have a suspicion as to how one might justify the claim), but which you have not addressed. I said nothing about $\lim_{n\to\infty} f_n(x,y)$. The $f_\infty$ function is just the indicator function for $\gamma$, and thus $\lim_{t\to1} f_\infty(\gamma(t))=1$, but, if that function is not 1 everywhere, $\lim_{(x,y)\to(0,0)} f_\infty(x,y)$ doesn't exist. – Glen O Mar 19 '17 at 04:13
2

Interesting nontrivial theorem (simplified version of teorema 5 in Límites utilizando coordenadas polares, La Gaceta de la RSME, v. 7, n. 2.):

Let be $f$ defined in a neighborhood of $(0,0)$, $F(r,\theta) = f(r\cos\theta,r\sin\theta)$. We have the following equivalence:

$$\lim_{(x,y)\to(0,0)}f(x,y) = L\iff \forall\bar{\theta}\in[0,2\pi] \lim_{(r,\theta)\to(0,\bar{\theta})}F(r,\theta) = L.$$ (the second limit isn't a directional limit)

The essential ingredient of the proof is that $[0,2\pi]$ is compact.

Martín-Blas Pérez Pinilla
  • 42,722
  • 4
  • 51
  • 94
  • 1
    I'm sorry, but I am not quite understanding here. You still have $r \to 0$ and $\theta \to \overline\theta$, so what have you gained? You still have a double limit to evaluate, and now even have to show that it converges for all values of $\overline\theta$. While I do not doubt it's truthfulness, it seems a step backwards for the OP rather than forwards. Am I misunderstanding something? – Paul Sinclair Mar 16 '17 at 03:27
  • @PaulSinclair, true, is a double limit. But with the change of variables can be easier than the original limit. – Martín-Blas Pérez Pinilla Mar 16 '17 at 07:05
  • In fact, @PaulSinclair should "doubt its truthfullness." It is false. https://math.stackexchange.com/questions/753381/limit-fracx2yx4y2-is-found-using-polar-coordinates-but-it-is-not-supp – JasonJones Oct 15 '20 at 22:58
  • 2
    @JasonJones - the error in that question was that edgaralienfoe converted the double limit to a single limit in $r$ while $\theta$ was held constant, The latter can converge for all $\theta$ and the double limit still fail to converge. Martín-Blas Pérez Pinilla is comparing a double limit in $(x, y)$ to a double limit in $(r,\theta)$, which is a different beast from what edgaralienfoe did. Martín-Blas is correct about the equivalence here. – Paul Sinclair Oct 16 '20 at 16:50
  • @PaulSinclair You are quite right. I was reading it as $(r,\overline{\theta}) \to (r,\overline{\theta})$ instead of the correct $(r,\theta) \to (r,\overline{\theta})$. This is actually a neat result. I'd love to see an example where this method works better than alternatives. – JasonJones Oct 18 '20 at 20:52
2

I am adding this because some are apparently having trouble understanding how to fill the details of Bananach's idea, and it cannot be explained in full in 500-character comments. It is not really an answer to the OP in my opinion, as while Bananach's method works in theory, it is entirely impractical for actual verification that given double limit converges, which appears to be what the calcstudent is after.

Still, it is a very nice theoretical result. So I hope you will forgive me for trying to give it the hearing I think it deserves. Of course I will include my modification that addresses Hurkyl's concerns.

We start with the well-known result of Peano.

Theorem: There exists a curve $\alpha : [0,1] \to [0,1]^2$ which is both continuous and surjective.

Proofs abound. For example: http://www4.ncsu.edu/~njrose/pdfFiles/HilbertCurve.pdf

A couple of quick but useful expansions:

Corollary: For any real $a,b,c,d$ with $a < b, c<d$, there is a curve $\alpha_1 : [0,1] \to [a,b]\times[c,d]$ which is continuous and surjective.

Proof: The map $f : [0,1]^2 \to [a,b]\times[c,d] : (x, y) \to (a + (b-a)x,~c + (d-c)y)$ is a continuous bijection, so $\alpha_1 = f\circ \alpha$ will do.

Corollary: For any real $a,b,c,d$ with $a < b, c<d$ and points $u, v \in [a,b]\times[c,d]$ there is a curve $\alpha_2 : [0,1] \to [a,b]\times[c,d]$ wich is continuous and surjective, with $\alpha_2(0) = u$ and $\alpha_2(1) = v$.

Proof: Since rectangles are convex, $$\alpha_2(t) = \begin{cases} u + 3t(\alpha_1(0) - u) & 0 \le t \le \frac 13\\ \alpha_1(3t - 1) & \frac 13 \le t \le \frac 23\\ \alpha_1(1) + (3t - 2)(v -\alpha_1(1)) & \frac 23 \le t \le 1\end{cases}$$ will work. (For those who may balk at the double definitions for the splices, I am asserting that the two definitions coincide, as is easily verified. This is useful for assuring continuity.)

Lemma: Let $A = \{(x,y) \in [-1,1]^2 : |x| \ge 1/2 \text{ or } |y| \ge 1/2\}$. Then there is a curve $\beta : [0,1] \to A$ which is continuous and surjective, with $\beta(0) = (1,1)$ and $\beta(1) = (1/2, 1/2)$.

Proof: Let $$B = [-1,1] \times [1/2,1]\\C = [-1, -1/2]\times[-1, 1/2]\\D = [-1/2, 1]\times[-1,-1/2]\\E = [1/2,1]\times[-1/2,1/2]$$ Then $A = B \cup C \cup D \cup E$.

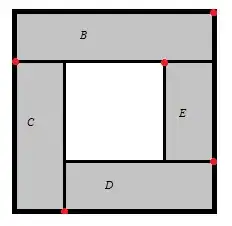
set A composed of sets B,C,D, and E

Therefore, by the previous corollary, there are continuous surjective curves $\beta_B : [0,1] \to B,~\beta_C : [0,1] \to C,~\beta_D:[0,1]\to D,~\beta_E:[0,1]\to E$ with $$\beta_B(0) = (1,1)\\\beta_B(1) = \beta_C(0) = (-1, 1/2)\\\beta_C(1) = \beta_D(0) = (-1/2, -1)\\\beta_D(1) = \beta_E(0) = (1, -1/2)\\\beta_E(0) = (1/2, 1/2)$$ Define $$\beta(t) = \begin{cases} \beta_B(4t) & 0 \le t \le 1/4\\ \beta_C(4t - 1) & 1/4 \le t \le 1/2\\ \beta_D(4t - 2) & 1/2 \le t \le 3/4\\ \beta_D(4t - 3) & 3/4 \le t \le 1 \end{cases}$$ Continuity and surjectivity of $\beta$ are clear.

Theorem: There is a continuous surjective curve $\gamma : [0,1] \to [-1,1]^2$ such that

  1. $\gamma(1) = (0,0)$ and for all $t < 1, \gamma(t) \ne 0$.
  2. for all $n \in \Bbb N$, $\gamma([1 - 2^{-n}, 1]) = [-2^{-n},2^{-n}]^2$

Proof: Define $\gamma(1) = 0$, and for all $k \in \Bbb N$ and $t \in [1-2^{-k},1-2^{-k-1}]$, define $$\gamma(t) = 2^{-k}\beta(2^{k+1}(t-1) + 2)$$ Since $\beta \ne (0,0)$ anywhere in its range, it follows that $\gamma(t) \ne (0,0)$ for these $t$. Since $\bigcup_{k\in\Bbb N} [1-2^{-k},1-2^{-k-1}] = [0,1)$, part 1 is satisfied, provided that $\gamma$ is well-defined.

Note that if $t = 1 - 2^{-n}$, then it lies in 2 of the intervals: either $k = n$ and $t = 1 - 2^{-k}$ is the lower endpoint, or $k = n-1$ and $t = 1- 2^{-k-1}$ is the upper endpoint. All other values of $t > 0$ lie in only one interval.

If $k = n$, then $$\gamma(t) = 2^{-n}\beta(2^{n+1}(-2^{-n}) + 2) = 2^{-n}\beta(-2+2) = 2^{-n}(1,1) = (2^{-n}, 2^{-n})$$ While letting $k = n-1$ gives $$\gamma(t) = 2^{1-n}\beta(2^n(-2^{-n}) + 2) = 2^{1-n}\beta(-1+2) = 2^{1-n}(1/2,1/2) = (2^{-n}, 2^{-n})$$

So $\gamma(t)$ is well-defined on the overlaps, and since $\gamma$ is continuous on each interval and has the same value on the overlaps, it follows that $\gamma$ is continuous everywhere on $[0,1)$.

Now if for some $n,~ 1 - 2^{-n} \le t < 1$, then there is an $k \ge n$ with $t \in [1-2^{-k},1-2^{-k-1}]$ and $$\gamma(t) \in 2^{-k}[-1,1]^2 = [-2^{-k},2^{-k}]^2 \subseteq [-2^{-n},2^{-n}]^2$$ since $[-1,1]^2$ is the codomain of $\beta$. Since $\gamma(1) = (0,0), we have $\gamma([1 - 2^{-n},1]) \subseteq [-2^{-n},2^{-n}]^2$

Conversely, if $(0,0) \ne (x,y) \in [-2^{-n},2^{-n}], let $k = min {m\mid 2^{-m-1} \le |x| \text{ or } 2^{-m-1} \le |y|}. Then $1 > |2^kx|, ~1 > |2^ky|$ (otherwise $k-1$ would be in the set), and at least one of $|2^kx|$ and $|2^ky|$ is $\ge 1/2$. So $(2^kx, 2^ky) \in A$, the codomain of $\beta$. Hence there is a $t_0 \in [0,1]$ with $\beta(t_0) = (2^kx, 2^ky)$. Let $t = 2^{-k-1}(t_0 - 2) + 1$. Then $1-2^{-k} \le t \le 1 - 2^{-k-1}$, and $\gamma(t) = (x,y)$. Since $k \ge n, 1-2^{-n} \le 1-2^{-k}$, and so $[-2^{-n},2^{-n}]^2 \subseteq \gamma([1-2^{-n},1])$, which proves condition 2.

All that remaims is to prove $\gamma$ is continuous at $1$. Let $\epsilon > 0$, and choose $n$ large enough that $[-2^{-n},2^{-n}]^2$ lies within the ball of radius $\epsilon$ about $(0,0)$. Let $\delta = 2^{-n}$. For $t\in[0,1]$, if $|1-t| < \delta$ then $t \in [1- 2^{-n},1]$, so $\gamma(t) \in [-2^{-n},2^{-n}]^2 \subseteq B_\epsilon((0,0))$ and so is continuous at $1$.

Finally, to address the question:

Theorem: Let $f$ be a real-valued function defined on a neighborhood of $(0,0)$ in $\Bbb R^2$. Then $$\lim_{(x,y)\to(0,0)} f(x,y)$$ converges if and only if $$\lim_{t\to 1} f\circ\gamma(t)$$ converges, in which case they have the same limit.

Proof: Since $\lim_{t\to1} \gamma(t) = (0,0)$, the convergence of the first limit implies the second. It remains to show that the convergence of the second implies the first.

Suppose that $\lim_{t\to 1} f\circ\gamma(t) = L$ and let $\epsilon > 0$. Then there is a $\delta_0$ such that if $1 - \delta_0 < t \le 1$ then $|f\circ\gamma(t) - L| < \epsilon$. And there is an $n$ such that $2^{-n} < \delta_0$. Let $\delta = 2^{-n}$. If $0 < |(x,y) - (0,0)| <\delta$, then in particular, $(x,y) \in [-2^{-n},2^{-n}]$ and so there is a $t \in [1- 2^{-n}, 1]$ such that $\gamma(t) = (x,y)$. Since $(x,y) \ne (0,0), t \ne 1$. So $0<|t - 1| \le 2^{-n} < \delta_0$, so $|f(\gamma(t)) - L| < \epsilon$. I.e., $|f(x,y) - L| < \epsilon$. Therefore $$\lim_{(x,y)\to(0,0)} f(x,y) = L$$ as required.

Paul Sinclair
  • 45,932