Can these kolams/rangoli be drawn mathematically in any programming language?

Question

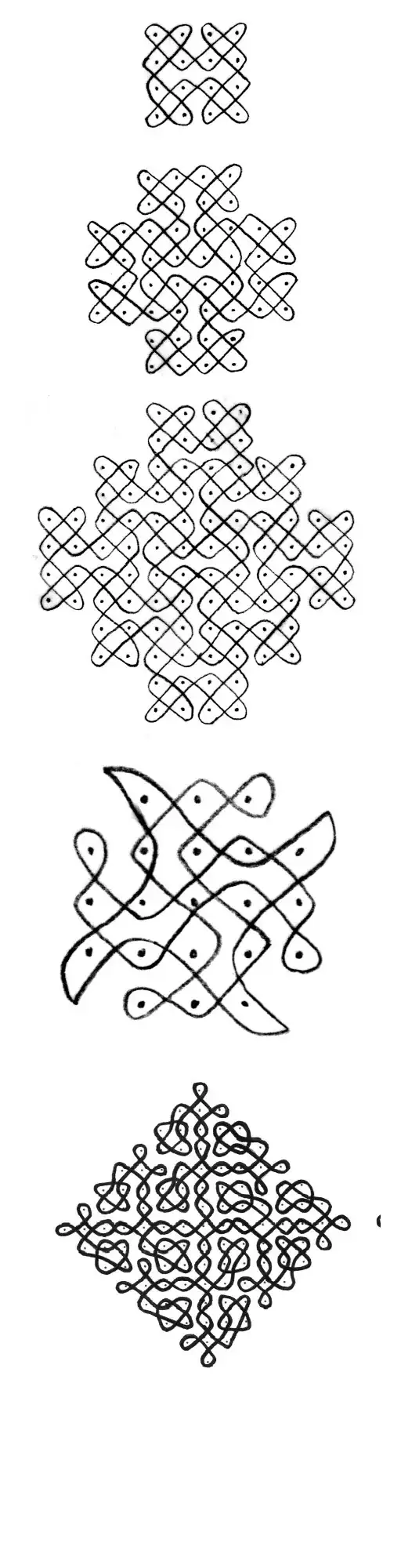
I would like to know how to draw these kolams/rangoli programmatically. in any language, what kind of math is required? They are fascinating works of symmetry, thus I feel it should be possible, but don't know where to start.

Answer 1

There is a research paper from Kiwamu Yanagisawa and Shijiro Nagata: "Fundamental Study on Design System of Kolam Pattern" e.g. here https://www.researchgate.net/publication/237442288_Fundamental_Study_on_Design_System_of_Kolam_Pattern

YANAGISAWA, Kiwamu & NAGATA, Shojiro. (2007). Fundamental Study on Design System of Kolam Pattern. "Kolam" is a kind of string/knot pattern seen primarily in Tamilnadu state of South India, which has a very attractive system of pattern formation, that is to say, countless complicated Kolam patterns can be drawn following extremely simple elements and drawing rules. In this paper, the fundamental characteristic of Kolam patterns' designing system is considered by converting these patterns into numbers and linear diagrams. Further discussions on the drawing methods to create new Kolams will also be given.

There is a set of 16 (sic) basic curve shapes at / around each dot which can be represented with the hexadecimal numbers 0x0 .. 0xF.

Table 1. 16 Constituent units of Kolam Patterns, corresponding to hexadecimal numbers.

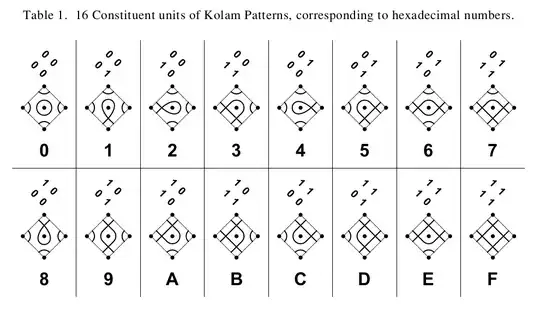
The shapes are called with names (circle, drop, saddle, pupil, fan and diamond) and can be described by a matrix of 4 bits (0, 0, 0, 0) to (1, 1, 1, 1). The least significant bit is the one which is defined for the lower, right corner in a 2*2 convolution. You have to slant this matrix 45° into the right hand direction, so the center point of the convolution is on the diagonal of the resulting 1-3-1 diamond shape. The LSB (Bit 0) is then the lower corner, Bit 1 is the left corner, Bit 3 is the right corner and MSB (Bit 4) is the top corner of this slanted 2x2 matrix or 1-3-1 diamond shape. Each bit signifies either no connection (tangent) or a crossing of the lines surrounding the 5 points. So with the four potential connections around each point we can create exactly 16 different elemental shapes which have designated names and symmetrical / mirror properties.

I tried to add a description of the individual shapes in Table 1 and its rotational and mirror symmetrical properties in the following list:

• 0 circle (N°, fully rotational symmetric)
• 1 drop (180°, upwards)
• 2 drop (270°, right)
• 3 saddle (225°)
• 4 drop (90°, left)
• 5 saddle (135°)
• 6 pupil (0°, 180° symmetry, horizontal mirror)
• 7 fan (0°, upright)
• 8 drop (0°, down)
• 9 pupil (90° / 180° symmetry, vertical mirror)
• A saddle (-45° / 315°)
• B fan (90°, right)
• C saddle (45°)
• D fan (270°, left)
• E fan (180°, down)
• F diamond (90° rotational symmetry)

With that "simple" language you can describe & define all possible Kolam pattern's that adhere to the given definition.

The authors continue on to review special properties of Kolam's with 5x5 and 7x7 diamond shapes:

Fig. 10. Pattern generation and one-stroke judgment. Table 2. Result of analysis on Kolam of 1-5-1 array of points.

Some of these special Kolam pattern's have a lot in common with convolution kernels used in image manipulation, pattern recognition, convolutional neural networks and deep learning. If you look at it from a 45° angle you can see how the convolution matrix and the underlying equations are calculated (e.g. in respect to FFT's).

See here a screenshot detailing the simple 3*3 vector convolution of (1,2,3) * (4,5,6) = (4,13,28,27,18) from a recent video by Grant "3 Blue 1 Brown" Sanderson

$(1+2x+3x^2)(4+5x+6x^2) = 4+13x+28x^2+27x^3+18x^4$

	$1$	$2x$	$3x^2$
$4$	4	8	12
$5x$	5	10	15
$6x^2$	6	12	18

3*3 convolution

But what is a convolution? https://www.youtube.com/watch?v=KuXjwB4LzSA

Answer 2

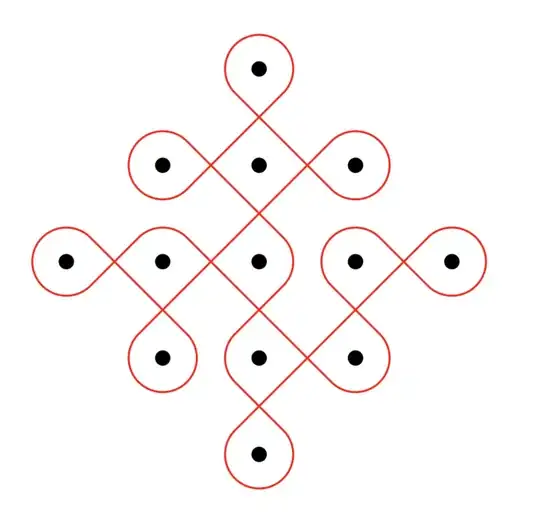
Just seeing this now, here is a LaTeX-Tikz code for the same.

\documentclass{article}
\usepackage{tikz} % Required for inserting images
\usetikzlibrary{shapes}
\usetikzlibrary{plotmarks}
\usetikzlibrary{calc,arrows,hobby}
\def\centerarc#1(#3:#4:#5) { \draw[#1] ($(#2)+({#5cos(#3)},{#5sin(#3)})$) arc (#3:#4:#5); }
\begin{document}
\begin{tikzpicture}
\filldraw (5,5) circle (3pt);
\filldraw (3.5858,5) circle (3pt);
\filldraw (2.1716,5) circle (3pt);
\filldraw (.7574,5) circle (3pt);
\filldraw (-.6568,5) circle (3pt);
\filldraw (3.5858,3.5858) circle (3pt);
\filldraw (.7574,3.5858) circle (3pt);
\filldraw (2.1716,3.5858) circle (3pt);
\filldraw (2.1716,2.1716) circle (3pt);
\filldraw (3.5858,6.4142) circle (3pt);
\filldraw (2.1716,6.4142) circle (3pt);
\filldraw (.7574,6.4142) circle (3pt);
\filldraw (2.1716,7.8284) circle (3pt);
%\draw [-,very thick] (-4,5) to[out=90,in=180]  (-2,6);
%\draw (-4,5) to[curve through={(-3,6)}] (-2.293,5.707);
%\draw (-2.293,5.707) to  (-2,5);
%\centerarcred,thick(215:45:1)
\centerarcred,thick(315:45:.5)
\draw [red,thick] (-.30325,5.35355) -- (1.1109,3.9393);
\centerarcred,thick(45:0:.5)
\centerarcred,thick(-180:0:.5)
\centerarcred,thick(135:180:.5)
\draw [red,thick] (.7574,4.2929) -- (3.2323, 6.7677);
\draw [red,thick] (.7574,4.2929) -- (.4039,3.9385);
\centerarcred,thick(0:135:.5)
\centerarcred,thick(225:360:.5)
\draw [red,thick] (3.2323,6.0607) -- (1.8181,7.4749);
\centerarcred,thick(0:225:.5)
\centerarcred,thick(315:360:.5)
\draw [red,thick] (2.5251,7.4749) -- (1.1109,6.0607);
\centerarcred,thick(45:315:.5)
\draw [red,thick] (2.5251,5.3535) -- (1.1109,6.7677);
\centerarcred,thick(315:405:.5)
\draw [red,thick] (2.5251,2.5251) -- (1.8181,3.2323);
\centerarcred,thick(135:225:.5)
\draw [red,thick] (2.5251, 4.6465) -- (1.8181,3.9385);
\centerarcred,thick(135:405:.5)
\draw [red,thick] (1.8180,2.5251) -- (4.6644,5.37);
\centerarcred,thick(225:495:.5)
\draw [red,thick] (4.6465,4.6465) -- (3.9393,5.3535);
\centerarcred,thick(45:225:.5)
\draw [red,thick] (3.2323,4.6465) -- (3.9391,3.9391);
\centerarcred,thick(225:405:.5)
\draw [red,thick] (3.2323,3.2323) -- (1.1109,5.3535);
\centerarcred,thick(45:135:.5)
\draw [red,thick] (.4039,5.3535) -- (-.3033,4.6465);
\end{tikzpicture}
\end{document}

Final Image: