28

The following story is true, not just to make it sound mysterious or coincidental. I found a very curious sequence of integers, and searching it gave no result. I am trying to learn more about it, just for fun.

We were taking a break with two friends, and came up with the following game in the staircase:

  • Assume there are $n$ stairs (so $n+1$ places to stand);
  • Starting from the bottom, go up 1 stair at a time, until you reach the top;
  • Then turn around and go down 2 stairs at a time, until you can't go further;
  • Then turn around and go up 3 stairs at a time, until you can't go further;
  • .. Then 4, 5, 6, etc. stairs at a time, until you can't even make one step.

Whatever the step size is when you stop (the one you cannot achieve), is characteristic of the number of stairs in the staircase, and we call it the Mona number (after my friend Mona).

For Example: For $n=5$ we go up to the top, then down in sets of $2$ until we reach $1$, then up $3$ to $4$, then down $4$ to $0$, then up $5$ to $5$, and then we are stuck because there aren't $6$ stairs to go down from our current position. Therefore $M(5)=6$.

From there, we wondered if we could find a formula for that number. Obviously it has to be at least 2 (going up the stairs one stair at a time should always be possible), but it is not monotonic with the number of stairs. The "mirroring" operation of "turning around" makes it quite difficult; in particular the system clearly has a memory, but the state of that memory does not only depend on the previous step size. So instead, we wrote a program for it (Matlab code):

function k = mona(n)

    assert( n >= 1 );    
    h = n;
    k = 2;

    while h >= k
        h = mod(h,k);
        h = n-h;
        k = k+1;
    end

end

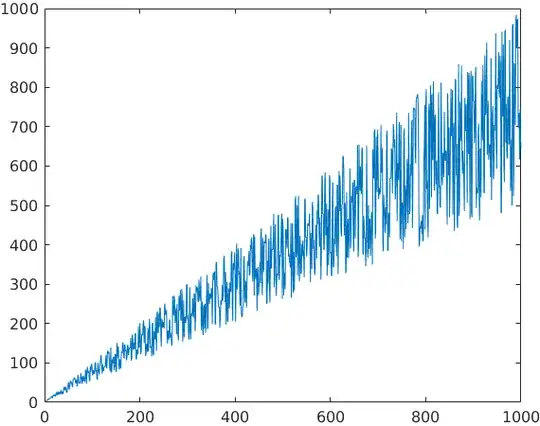
where n is the number of stairs, k is the step size, and h is the "horizon" -- aka the number of stairs remaining until the end of the staircase for a given step size. Plotting it for the first 1000 integers looks like this:

Mona sequence for the first 1000 integers

I have thought about it for a while, but it is much more complicated to analyse than it seems, and the analytic formulation of the sequence is ugly so I'm not sure it can help.

I would be curious to know whether this relates to any known integer process? And if not, whether you have a clever idea of how to analyse the Mona sequence?

About the envelope

As can be seen on the plot, there seems to be a bounding cone to the progression of this sequence. This "envelope" corresponds to the following cases (found programmatically):

\begin{align} N_\mathrm{upper} &= \left\{ n\ |\ M(n)=n+1 \right\} = \{ 1,2,5,8,14,50,119,200,269,299, ... \} \\ N_\mathrm{lower} &= \left\{ n\ |\ M(n)=\left\lceil \frac{n}{2}\right\rceil + 1 \right\} = \{ 1,3,7,39,47,111,959, ... \} \end{align}

However once again, neither of these sequences give a hit in the OEIS.

Blue
  • 83,939
Jonathan H
  • 2,343
  • "Whatever your step size then, is characteristic of the number of stairs in the staircase, and we call it the Mona number (after my friend Mona)." I don't understand this sentence. I thought we were varying the step size across all integers? – Stella Biderman Feb 15 '17 at 18:20
  • @StellaBiderman Probably that means the first step size for which you cannot move a single time is uniquely determined by number of stairs alone, as in if $n=1$ once you go to top you cannot move again because you'd have to step down 2 stairs which cannot happen, so first term is $2$ and so on – user160738 Feb 15 '17 at 18:22
  • @StellaBiderman Sorry if my explanation is unclear; for a given number of stairs, the game is to gradually increase the step-size going up and down the stairs. This gives the Mona number. If you repeat this game for an increasing number of stairs, then you get the Mona sequence. Does that help? – Jonathan H Feb 15 '17 at 18:23
  • 1
    Oh I see, so, for $n=5$ we go up to the top, then down in sets of $2$ until we reach $1$, then up $3$ to $4$, then down $4$ to $0$, then up $5$ to $5$, and then we are stuck because there aren't $6$ stairs to go down from our current position or $7$ stairs to go up? So $M(5)=5$ – Stella Biderman Feb 15 '17 at 18:25
  • @StellaBiderman Yes, well M(5)=6 because that's the step-size you cannot achieve :) But you can shift the whole sequence by one if it makes more sense to you (just add the line k=k-1 after the while loop in the program). – Jonathan H Feb 15 '17 at 18:26
  • If I cannot go up again, but can go down (perhaps I'm at $(n+10)/2$ and am trying to move up $n/2$) do I stop where I am the first time I can't take a step, or can I take $0$ steps up and then one step down and continue until I cannot move in either direction? – Stella Biderman Feb 15 '17 at 18:28
  • @StellaBiderman As it is presently defined, you stop the first time you cannot take a step. Since the previous step-size is always smaller, I cannot actually imagine a situation where this would happen though. – Jonathan H Feb 15 '17 at 18:30
  • 1
    Let's say we define $M(a,b)$ to be where you are after you make the $b^{th}$ step on a staircase of size $a$ and use the convention that there is a $0^{th}$ step. Then $M(a)\leq a+1$ and $$M(a)=a+1\iff M(a,a-1)=0\iff M(a, a-2)=a-1\iff\cdots$$ The larger $a$ is the longer you can expand this equality condition, because it holds for $b>a/2$ (since that guarantees that you're only taking one step each time) – Stella Biderman Feb 15 '17 at 18:37
  • Maybe look at those cases for which $M(a)=a+1$? OEIS turned up 19 sequences with the first five: $1,2,5,8,14$ and 20 with the first five plus one: $2,3,6,9,15$. – John Feb 15 '17 at 18:48
  • 1
    @John, no results if you use more terms: $(2,3,6,9,15,51,120,201)$ or $(1,2,5,8,14,50,119,200)$. – Peter Kagey Feb 15 '17 at 18:55
  • Thanks for tying a bow on it @PeterKagey (I didn't have the means currently to code it up). – John Feb 15 '17 at 19:09
  • 1
    @John and Peter, I edited the OP to include something about the apparent envelope. Perhaps it makes more sense to subtract 1 to this sequence, seeing as the formulas always seem to carry a +1 so far. – Jonathan H Feb 15 '17 at 19:18
  • @Sheljohn, I did just that with A282443: The largest step that is taken (rather than the smallest step that cannot be taken). – Peter Kagey Feb 15 '17 at 21:11
  • 1
    @Sheljohn: (+1) especially for this nice and insightful presentation! – Markus Scheuer Feb 16 '17 at 08:00

1 Answers1

5

I would be curious to know whether this relates to any known integer process?

This reminds me of the Fibonacho's sequence (A280521) which was asked on Reddit by user Teblefer—and more specifically, it reminds me of the natural number generalization: A057945.

The Fibonacho's sequence works similarly (quote from the Reddit post):

two people are sharing a plate of nachos. They take turns dividing the nachos, each taking the nth Fibonacci number of nachos on the nth turn. When the number of nachos left is less than the next Fibonacci number, they start the sequence over. What number of nachos (less than 500) requires the most number of restarts? How would you generate numbers of nachos with a high number of restarts?

In a recent lecture, Neil Sloane (the founder of the OEIS) discusses the Fibonacho's sequence and its generalizations. (You can see the details in Slides 18-23 and the video starting at 12:50.)

In general, Neil suggests that there has not been much exploration of (or insight into) these Fibonacho-like problems, which leads me to believe that the "Mona" sequence is probably largely unexplored too.

I've gone ahead an added these and related sequences to the OEIS and linked them back to this question.

  • A282442: smallest step size that does not occur.
    • 2, 3, 3, 4, 6, 5, 5, 9, 9, 8, 10, 11, ...
  • A282443: largest step size that does occur.
    • 1, 2, 2, 3, 5, 4, 4, 8, 8, 7, 9, 10, ...
  • A282444: Numbers $n$ such that $A282442(n) = n + 1$.
    • 1, 2, 5, 8, 14, 50, 119, 200, 269, 299, 1154, 5369, ...
  • A282427: Numbers $n$ such that $A282442(n) = \lceil\frac{n}{2}\rceil + 1$.
    • 1, 3, 7, 39, 47, 111, 959, 3319, 7407, 11967, 13007, 16239, ...
  • A282434: Positions of records in A282442.
    • 1, 2, 4, 5, 8, 11, 12, 14, 18, 19, 21, 24, ...
  • A282573: Number of steps taken.
    • 1, 3, 4, 7, 10, 12, 13, 19, 20, 23, 26, 32, ...
  • A282574: Final position.
    • 1, 0, 1, 3, 5, 2, 3, 0, 1, 7, 9, 2, 3, 0, ...
Peter Kagey
  • 5,438
  • I will have a look at the Fibonacho sequence :) If you are right, then perhaps there is little chance that my question will be answered in the near future. – Jonathan H Feb 15 '17 at 19:20