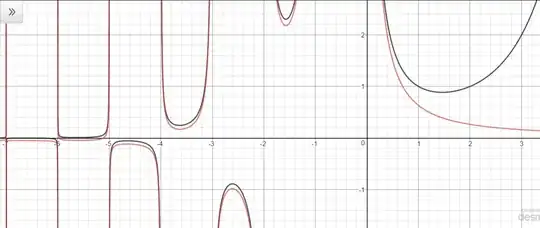
This series differs from $\Gamma(x)$ by an analytic function. For $\Re(x)>0$,
$$ \Gamma(x) = \int_0^{\infty} t^{x-1} e^{-t} \, dt \\
= \int_0^1 t^{x-1} e^{-t} \, dt + \int_1^{\infty} t^{x-1} e^{-t} \, dt \\
= f(x) + \Gamma(1,x), $$
by expanding the exponential as a power series and integrating term-by-term. $\Gamma(1,x)$ is the upper incomplete Gamma-function, and is an analytic function of $x$, while your series is the lower incomplete Gamma-function $\gamma(1,x)$. Meromorphic continuation implies that the equality derived above holds whenever $x$ is not a nonpositive integer: one can show that $f(x)$ is locally uniformly convergent on domains avoiding the nonpositive integers, so is a meromorphic function, and the result follows.
Notably, it is easy to check using integration by parts that $\Gamma(1,x)$ is exponentially small for $x \ll 0$, hence why the dominant behaviour on the left is captured by $f$. On the other hand, $f$ is much smaller than the exponentially large $\Gamma(1,x)$ for $x \gg 0$, so $\Gamma(1,x)$ is dominant on the right.
For more information, you can also see this answer I wrote a while ago.