Let's calculate first the whole value of $I$ over the rectangle $\mathcal D=[a,X]\times[b,Y]$, we integrate over $y$ first.
$\displaystyle I(\mathcal D)=\int_a^X\int_b^Y(x+y)dxdy$
$\displaystyle =\int_a^X\bigg[xy+\frac{y^2}{2}\bigg]_b^Ydx=\int_a^Xx(Y-b)+\frac{Y^2-b^2}{2}dx$
$\displaystyle =\bigg[\frac{x^2}{2}(Y-b)+\frac{Y^2-b^2}{2}x\bigg]_a^X=\frac{X^2-a^2}{2}(Y-b)+\frac{Y^2-b^2}{2}(X-a)$
$\displaystyle =\frac{XY}{2}(X+Y)-\frac{b}{2}X^2-\frac{a}{2}Y^2-\frac{b^2}{2}X-\frac{a^2}{2}Y+\frac{ab}{2}(a+b)$
This is all symmetrical in $a,b,X,Y$, and obviously the result will be the same if we integrate over $x$ first.
So we can see that the primitive obtained without specifying any domain of integration is in fact
$$F(X,Y)=\frac{XY}{2}(X+Y)=I(\mathcal D_0)$$ where $\mathcal D_0=[0,X]\times[0,Y]$ for $a,b=0$.
Your change of variables is the following:
$\begin{pmatrix} x\\ y\\ \end{pmatrix}=\begin{pmatrix} u+v\\ u-v\\ \end{pmatrix}=\begin{pmatrix}1 & 1\\ 1 & -1\\ \end{pmatrix}\begin{pmatrix} u\\ v\\ \end{pmatrix}$ and jacobian $|J|=|-1-1|=2$
In regards to the previous explanation, when you calculate
$\displaystyle G(U,V)=\iint_{\mathcal W_0} 2u\,|J|\ dudv=\bigg[2u^2v\bigg]_{\mathcal W_0}=2U^2V$
you implicitly do it over the domain $\mathcal W_0=[0,U]\times[0,V]$.
Before studying your change of variables, let's have a look at a simple rotation by angle $\theta=-45°$.
$\begin{pmatrix} u\\ v\\ \end{pmatrix}=
\begin{pmatrix}\cos(\theta) & -\sin(\theta)\\ \sin(\theta) & \cos(\theta)\\ \end{pmatrix}\begin{pmatrix} x\\ y\\ \end{pmatrix}=
\begin{pmatrix}\frac{1}{\sqrt 2} & \frac{1}{\sqrt 2}\\ -\frac{1}{\sqrt 2} & \frac{1}{\sqrt 2}\\ \end{pmatrix}\begin{pmatrix} x\\ y\\ \end{pmatrix}=
\frac{1}{\sqrt 2}\begin{pmatrix} y+x\\ y-x\\ \end{pmatrix}$
Now if you change the frame $(\vec x,\vec y)$ to the rotated frame $(\vec u,\vec v)$ then the domain $\mathcal D_0$ will simply transform into the rotated rectangle $\mathcal E_0$ of same length and width.
Thus $\mathcal E_0=[0,X]\times[0,Y]$ in the new frame $(\vec u,\vec v)$.
Where the rotation differs from integral change of variables, is that the plane $(x+y)$ is transported to the plane $(u+v)$ by the rotation.
Which obviously leads to the same value of the integral :
$\displaystyle \iint_{\mathcal D_0}(x+y)dxdy=\iint_{\mathcal E_0}(u+v)dudv$
So finally what is wrong will all this ?
Your change of variable is pretty close to the rotation case we have seen, in that case the rectangular domain $\mathcal D_0$ was transformed to another rectangular domain $\mathcal E_0$ but the inners of the integral were unchanged [ $(x+y)dxdy\to (u+v)dudv$ ].
We have seen also that the primitives $F(X,Y)$ and $G(U,V)$ without specifying the domain were equivalent to calculating them over the respective domains $\mathcal D_0$ and $\mathcal W_0$.
The catch in that, is that the theorem for the change of variables, ensures that $F(X,Y)=G(U,V)$ only if $\mathcal D_0$ is transformed into $\mathcal W_0$ by this change of variables.
The issue is that $\mathcal D_0=[0,X]\times[0,Y]$ does not changes to any $\mathcal W_0=[0,U]\times[0,V]$
(and certainly not to $[0,\frac{X+Y}{2}]\times[0,\frac{X-Y}{2}]$ either)
So let's have a look at the shape, $\mathcal D_0$ transforms into (obviously this will be some kind of rotated rectangle with change of orientation).
$\begin{cases}
(x,y)=(0,0)\to(u,v)=(0,0)\\
(x,y)=(X,0)\to(u,v)=(\frac{X}{2},\frac{X}{2})\\
(x,y)=(0,Y)\to(u,v)=(\frac{Y}{2},-\frac{Y}{2})\\
(x,y)=(X,Y)\to(u,v)=(\frac{X+Y}{2},\frac{X-Y}{2})\\
\end{cases}$
We can see (as expected), that it is not an $[0,U]\times[0,V]$ for any $U,V$.
Since the integral is symmetric in $x,y$ we do not lose generality in assuming $0\le Y\le X$ (else invert the role of $x$ and $y$), so we can have a drawing to support the study.
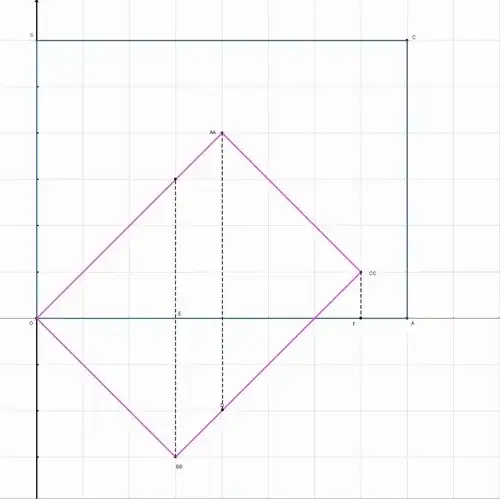
As you can see the blue rectangle $\mathcal D_0$ is transformed into the pink rectangle $\mathcal R$, but it is not supported by horizontal and vertical axis any more.
Yet, let now split along the dash lines:
$\mathcal R$ can be decomposed into $3$ compliant domains
$\begin{cases}
u\in[0,\frac{Y}{2}] & v\in[-u,u]\\\\
u\in[\frac{Y}{2},\frac{X}{2}] & v\in[u-Y,u]\\\\
u\in[\frac{X}{2},\frac{X+Y}{2}] & v\in[u-Y,X-u]\\
\end{cases}$
$\displaystyle I_1=\int_0^\frac{Y}{2}\int_{-u}^u2u\ dudv=\int_0^\frac{Y}{2}4u^2du=\bigg[\frac{4}{3}u^3\bigg]_0^\frac{Y}{2}=\frac{Y^3}{6}$
$\displaystyle I_2=\int_\frac{Y}{2}^\frac{X}{2}\int_{u-Y}^u2u\ dudv=\int_\frac{Y}{2}^\frac{X}{2}2uYdu=\bigg[u^2Y\bigg]_\frac{Y}{2}^\frac{X}{2}=\frac{X^2Y}{4}-\frac{Y^3}{4}$
$\displaystyle I_3=\int_\frac{X}{2}^\frac{X+Y}{2}\int_{u-Y}^{X-u}2u\ dudv=\int_\frac{X}{2}^\frac{X+Y}{2}2u(X+Y-2u)du=\bigg[u^2(X+Y)-\frac{4}{3}u^3\bigg]_\frac{X}{2}^\frac{X+Y}{2}=\frac{Y^3}{12}+\frac{XY^2}{4}$
$\begin{align}\displaystyle \iint_{\mathcal R}2u\,|J|\ dudv=2\times(I_1+I_2+I_3)&=2\times\left(Y^3\left(\frac{1}{6}-\frac{1}{4}+\frac{1}{12}\right)+\frac{X^2Y}{4}+\frac{XY^2}{4}\right)\\&=\frac{XY}{2}(X+Y)\end{align}$
Finally we have $$\iint_{\mathcal R}2u\,|J|\ dudv = \iint_{\mathcal D_0}(x+y)\ dxdy$$
It is important thus to understand that a change of variable, is not simply a change of frame that transport $(\vec x,\vec y)$ to $(\vec u,\vec v)$ but an operation in which the domain of integration matters and is affected by the transformation.
Specifically when you write a primitive as a n-dimensional integral without bounds, then it implicitly refers to the integral over the cuboid domain $\prod\limits_i [0,X_i]$ and you cannot assume it will simply transport to another cuboid domain $\prod\limits_i [0,U_i]$ by performing the variables change $(x_i)_i\to(u_i)_i$.
This is indeed this mistake that you are doing when calculating a primitive in $(u_i)_i$ variables by the integral without bounds.
When calculating over the properly transformed domain $\mathcal D_0\to\mathcal R$, we have seen in our particular example, that we were able to find the same result.
Remark:
The reason we do not have this issue in dimension $1$, is because an interval is always transformed into another interval by a continuous bijective change of variable. While in dimension $2$ a rectangle is not necessarily another rectangle with sides parallel to axis of coordinates...
