NN Backpropagation: Computing $\frac{{\rm d}E }{{\rm d}y}$.

Question

I would appreciate some help on the following problem: I'm taking Hinton's coursera class on Neural Nets and I'm not sure I understand the step highlighted in the picture (see below).

Background:

• $i$ is hidden layer
• $j$ is the top layer
• Neurons use logistic regression as their activation function

What I understand:
The chain rule allows you to "break down" the partial derivative and introduce a term that is helpful for your calculation:

$$\frac{\partial E}{\partial y_i}=\frac{\partial E}{\partial z_j}\cdot\frac{\partial z_j}{\partial y_i}$$

What I don't understand:
Where does the $\sum_j$ come from? In other words, what's the proof that you can break down the left term into the sum of 3 components of the top layer (in this case).

Thanks for your help.

Link to class: https://www.coursera.org/learn/neural-networks/lecture/gcNo6/the-backpropagation-algorithm-12-min

Answer 1

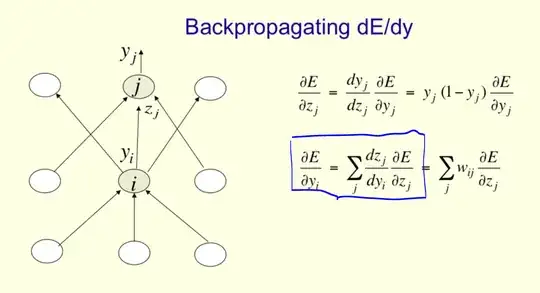
This follows from the multivariate chain rule. Let's assume that $E$ depends on $z=(z_1,\ldots,z_n)$, but each $z_k$ depends on $y=(y_1,\ldots,y_m)$, i.e. $$ E(z(y))=E(z_1(y),\ldots,z_n(y)). $$ We are interested in how the loss objective $E$ depends on some value in an earlier layer, say the output of the $i$th node, denoted $y_i$, in layer $\xi$, but that output affects $E$ only by its influence on the next layer (i.e., $\xi+1$), whose values we denote $z$. Recall that in a fully connected network, each layer depends on all the values of the previous layer, so each $z_i$ depends on each $y_k$. But we only care about $y_i$ for now, meaning we can ignore the other $y_k$, because we are interested in how perturbing $y_i$ affects $E$, and $y_i$ does not affect $E$ via the other $y_k$.

But $y_i$ does affect $E$ through $z$ (and only through $z$ actually). And $y_i$ affects every $z_k$. So we need to take the $\partial E / \partial z_k$ into account, as well as the $\partial z_k / \partial y_i$. The way to combine these into a single number is specified by the multivariate chain rule: $$ \frac{\partial E}{\partial y_i} = \sum_j \frac{\partial E}{\partial z_j} \frac{\partial z_j}{\partial y_i}. $$ I'll add links to more formal derivations below. But the rough intuition is this: $E$ depends on $y_i$ through its effect on each $z_k$ (captured by $\partial z_k / \partial y_i$), so ${\partial E}/{\partial y_i}$ should be a sum of these contributions (if we think of derivatives as a measure of local linear change, we can imagine adding the perturbation vectors induced by tweaking together). But not all the contributions to the network are equally important: if a $z_j$ doesn't affect $E$ much (i.e.,${\partial E}/{\partial z_j}$ is small), then the contribution of $y_i$ through $z_j$ should be down-weighted. So we do a weighted sum over $\partial z_k / \partial y_i$, with weights given by ${\partial E}/{\partial z_j}$. Notice that when $n=1$ we recover the classical chain rule. For more details see the links below.

---

Other questions on the origin of the multivariate chain rule are here, here, and here.

A related question on the role of the chain rule sum in artificial neural networks is here.