7

Consider integrating the following function of a complex variable, $z$,

$$ f(z)=\frac{z e^{irz}}{\sqrt{z^2+m^2}}, $$

around the contour

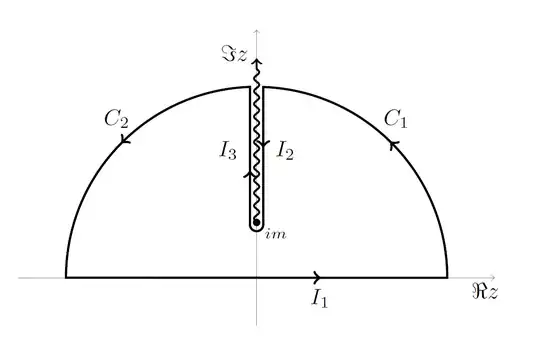
shown here

It seems straightforward to show that the infinite radius arc segments, $C_1$ and $C_2$, vanish and we are left with

$$ 0=I_1+I_2+I_3, $$

via the residue theorem. Now, I expect that the integrals along each side of the branch cut which runs from $im$ to $i\infty$ will differ "by a phase" so that they will add together rather than cancel. However, I don't see how to show this explicitly:

\begin{align} I_2 & = \int^m_\infty \frac{Re^{i\pi/2}}{\sqrt{R^2e^{i\pi}+m^2}}e^{irRe^{i\pi/2}}e^{i\pi/2}dR \\ & = \int^\infty_m \frac{R}{\sqrt{-R^2+m^2}}e^{-rR}dR \\ \end{align}

But

\begin{align} I_3 &= \int^\infty_m \frac{Re^{i3\pi/2}}{\sqrt{R^2e^{i3\pi}+m^2}}e^{irRe^{i3\pi/2}}e^{i3\pi/2}\\ &= -\int^\infty_m \frac{R}{\sqrt{-R^2+m^2}}e^{rR}dR, \end{align} so it appears $I_2\ne I_3$ which I believe to be wrong.

Parcly Taxel
  • 105,904
user143410
  • 427

1 Answers1

5

$$I_2 = i \int_{\infty}^m dy \, \frac{i y \, e^{-r y}}{+i \sqrt{y^2-m^2}} $$

$$I_3 = i \int_m^{\infty} dy \, \frac{i y \, e^{-r y}}{-i \sqrt{y^2-m^2}} $$

The difference in phase comes from how we define the behavior of the square root in the vicinity of the branch cut $[i m,i \infty)$. So the contributions from $I_2$ and $I_3$ add.

One should not necessarily ignore the contribution around the branch point where $z=i m + \epsilon e^{i \phi}$, $\phi \in [\pi/2,-3 \pi/2]$:

$$I_4 = i \epsilon \int_{\pi/2}^{-3 \pi/2} d\phi \, e^{i \phi} \frac{\left (i m +\epsilon e^{i \phi} \right ) e^{i r \left (i m +\epsilon e^{i \phi} \right )} }{\sqrt{m^2+\left (i m +\epsilon e^{i \phi} \right )^2}}$$

which indeed vanishes as $\epsilon \to 0$. Thus, by Cauchy's theorem we have the relation

$$\int_{-\infty}^{\infty} dx \frac{x \, e^{i r x}}{\sqrt{m^2+x^2}} = i 2 \int_m^{\infty} dy \, \frac{y \, e^{-r y}}{\sqrt{y^2-m^2}} = i 2 m K_1(r m)$$

Ron Gordon
  • 141,538
  • Indeed, I should have mentioned that the branch point does not contribute. So, am I to understand that the minus sign comes from our definition of the square root on each side of the branch cut (i.e., we put it in "by hand") as opposed to coming directly from the argument of z as I have attempted here (where, in fact, I took the wrong phase angle, anyway, it would seem) ? – user143410 Jan 28 '17 at 02:17
  • btw, I already had a question related to the very last equality you wrote which relates this to the Bessel function. It's submitted here – user143410 Jan 28 '17 at 02:24
  • @user143410: yes, that's right. There is a $2 \pi$ phase jump across a branch cut; in this case, in the opposite direction as we are traversing clockwise around the cut. This explains why we go from a $+$ to a $-$. To get the Bessel, just sub $y=m \cosh{t}$. – Ron Gordon Jan 28 '17 at 02:30
  • Yeah, I think that substitution would relate it to a different integral representation of the Bessel function than I want to use. I was trying to see how to put it in the same form as one finds in the "timelike" case, where the $r$ is being interpreted as a spacetime distance for the Klein Gordon propagator. – user143410 Jan 28 '17 at 02:36