Does anyone know if there is a name for the curve which is a helix, which itself has a helical axis? I tried to draw what I mean:
Asked
Active
Viewed 4,791 times
39
-
4Standard terms are 'super-helix' or 'super-coil'. See DNA. – amI Jan 18 '17 at 21:59
-
1But DNA is a double helix, which is a different thing from this. – user50229 Jan 19 '17 at 19:40
-
@aml the term supercoil includes other forms of secondary coiling, such as plectonemes, which are different from the example OP gave. So maybe it is a subset of supercoils. – Bitwise Jan 19 '17 at 20:12
-
1@user50229: True, but DNA also super-coils. https://www.youtube.com/watch?v=N5zFOScowqo – LarsH Jan 19 '17 at 20:27
-
2Informally, people might understand the analogy with a telephone wire – Ovi Jan 20 '17 at 00:12
-
@Jyrki I don't see anywhere in the thread where the name of the curve is given. – user50229 Jan 20 '17 at 09:49
-
1Ah! You wanted a name rather than a parametrization. Ok, sorry. – Jyrki Lahtonen Jan 20 '17 at 10:09
-
I believe this is the shape of a tungsten light bulb filament. – richard1941 Jan 25 '17 at 18:57
5 Answers
53
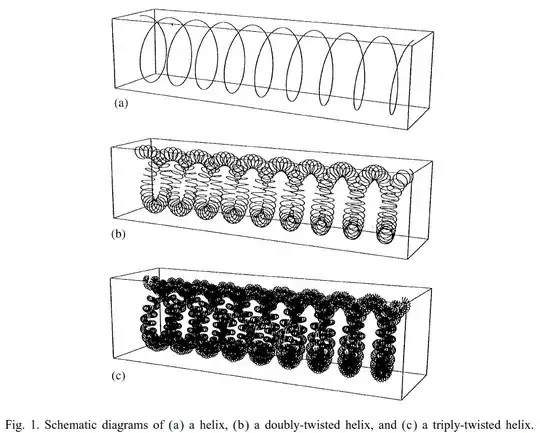
According to this journal article, we may call it a doubly-twisted helix or generally a multiply-twisted helix.
Ng Chung Tak
- 19,693
40
For a light bulb the wire is called a "coiled coil filament" in this Wikipedia article.
The German word is "Doppelwendel" (roughly translated: double screw).
mvw
- 35,114
-
6
-
5@rschwieb Even more fascinating: Tungsten is brittle, and still they manage to coil it like that. See https://www.youtube.com/watch?v=DIGqBb3iZPo – Arthur Jan 19 '17 at 23:34
22
I don't believe there is a standard term. Nevertheless, MathWorld calls the resulting curve a "slinky".
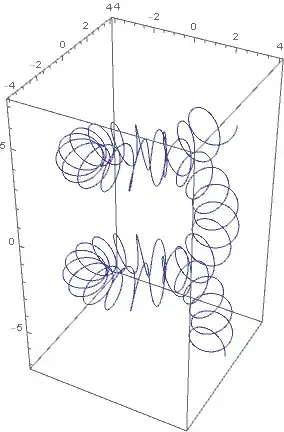
Of course, one can have a "slinky" of a "slinky":
J. M. ain't a mathematician
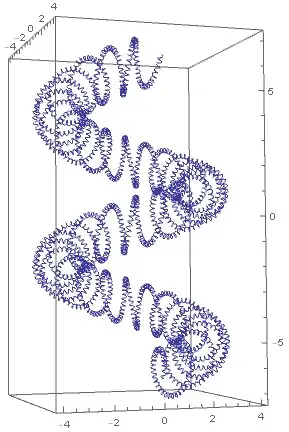
- 76,540
-
-
Since "slinky" = "superhelix", the last one can be called a superslinky? – user21820 Jan 19 '17 at 11:28
-
2Personally, I prefer the parametrization like this: \begin{bmatrix} a\cos t+r\left(\frac{b}{\sqrt{a^2+b^2}} \sin t \sin nt-\cos t \cos nt \right) \ a\sin t+r\left(\sin t \cos nt-\frac{b}{\sqrt{a^2+b^2}} \cos t \sin nt \right) \ bt+\frac{a}{\sqrt{a^2+b^2}} r\sin nt \end{bmatrix} with the parent/primary helix as: \begin{bmatrix} a\cos t \ a\sin t \ bt \end{bmatrix} – Ng Chung Tak Jan 19 '17 at 11:41
-
@Ng, yeah, I'd have made an arclength parametrization of the helix first so that the normal and binormal vectors would come out nice... – J. M. ain't a mathematician Jan 19 '17 at 12:49
-
P.S. The plots were of course generated with Mathematica. – J. M. ain't a mathematician Jan 19 '17 at 15:38
-
1J.M. Ng's formula is ok for the first iteration because the natural parameter is a constant multiple of $t$ (as I'm sure you know), so simple normalization of the normal/binormal will do just fine. You are, of course, right about the need to use arclength parametrization in all the succeeding iterations - I don't want to do that with paper&pencil :-) – Jyrki Lahtonen Jan 20 '17 at 07:44
-
"I don't want to do that with paper & pencil" - I'm sure you don't, @Jyrki. Mathematica actually gags if I try to iterate beyond the fifth, as the required Frenet frame expression is incredibly complex. – J. M. ain't a mathematician Jan 20 '17 at 12:52
8
A corresponding construction on the torus is called an "iterated torus knot", so perhaps "iterated helix" would be a good name. I don't know of any standard name.
John Hughes
- 100,827
- 4
- 86
- 159
5
Coiled coil as others also stated. More length is packed in a small volume. Used for electric bulb filaments, toroidal transformer primaries etc. Polar orbits of sun synchronous satellites around earth/sun is another example if the inner coil has no torsion.
EDIT1
A constant vector component of binormal is added to central coil vector if helicoids are to be defined as a surface... as a set of connected coils.
Narasimham
- 42,260