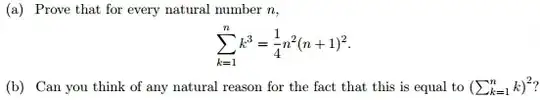Proving the sum of cubes?

Question

(a) Prove that for every natural number $n$, $$\sum_{k=1}^n k^3 = \frac14 n^2(n+1)^2.$$

(b) Can you think of any natural reason for that fact that this is equal to $\left(\sum_{k=1}^n k^2\right)$?

I'm really stuck as to where to start, I know I could probably google the first part but how does it relate to the second part?

Thanks in advance!

You can find also proof by induction here. This is one of sums which is asked here frequently. Also searching using Approach0 might help you to find similar questions. — Martin Sleziak, Jan 05 '17 at 15:18
For some basic information about writing math at this site see e.g. here, here, here and here. — Martin Sleziak, Jan 05 '17 at 15:18

score 1 · Answer 1 · answered Jan 05 '17 at 13:29

1

Hint 1:

$$(k+1)^3-k^3=3k^2+3k+1 \rightarrow \sum_{k=1}^{n} [(k+1)^3-k^3]=3\sum_{k=1}^{n} k^2+3\sum_{k=1}^{n} k+\sum_{k=1}^{n} 1$$

Hint 2:

You also can use induction.

Can you finish?

answered Jan 05 '17 at 13:29

Arnaldo

21,758

score 1 · Accepted Answer · answered Jan 05 '17 at 13:33

You can prove this by induction.

First, show that this is true for $n=1$:

$\sum\limits_{k=1}^{1}k^3=1^2(1+1)^2/4$

Second, assume that this is true for $n$:

$\sum\limits_{k=1}^{n}k^3=n^2(n+1)^2/4$

Third, prove that this is true for $n+1$:

$\sum\limits_{k=1}^{n+1}k^3=$

$\color\red{\sum\limits_{k=1}^{n}k^3}+(n+1)^3=$

$\color\red{n^2(n+1)^2/4}+(n+1)^3=$

$(n+1)^2(n+2)^2/4$

Please note that the assumption is used only in the part marked red.

Proving the sum of cubes?

2 Answers2