Suspect unfair die

Question

If I claim to have a fair die that rolls 1-6 uniformly but my die actually only rolls 1-5 uniformly (and never produces a 6) how many rolls would you need to see before you had over 50% confidence that I was messing with you?

Answer 1

You just need to compute the number of rolls that gives a $50\%$ chance of getting at least one $6$ on the assumption that it is a standard die. That corresponds to less than $50\%$ chance of having no $6$s. Can you do that?

Answer 2

Power Computation for a Chi-squared Goodness-of-Fit Test: Detecting an Unfair Die

Perhaps you are using the chi-squared goodness-of-fit (GOF) test, with test statistic $$Q = \sum_{i=1}^6 \frac{(X_i - E_i)^2}{E_i},$$ where $X_i$ is the number of occurrences of face $i$ in $n$ tosses of the die and $E_i = n/6$ is the expected number of occurrences of each face for a fair die. Notice that $Q = 0$ in the (unlikely) event that each face appears exactly 1/6 th of the time. The worse the agreement, the larger $Q$ becomes. (Although it is called a 'goodness-of-fit statistic', it is large for 'bad' fits.)

Then for a fair die, $Q \stackrel{aprx}{\sim} Chisq(df = \nu)$ provided $n$ is large enough that the expected counts exceed 5 (so you need $n/6 > 5$ and $n > 30).$ You have $k = 6$ categories and $\nu - k-1 = 6-1 = 5$ degrees of freedom.

It is typical to test at the 5% level of significance. You will reject the null hypothesis that the die is fair at the 5% level if $Q > q^*,$ where the 'critical value' $q^*$ is chosen to cut 5% from the upper tail of $Chisq(5).$ From tables or from R statistical software, you have $q^* = 11.07.$

 q.crit = qchisq(.95, 5);  q.crit
 ## 11.0705

However, for the dishonest die you describe, values of $Q$ are inflated and do not have the distribution $Chisq(5)$. The result is that you will reject the null hypothesis more often than 5% of the time, if you judge your dishonest die using the test described above.

In particular, you have asked to have a rejection rate of 50% instead of 5% when your dishonest die is used. To find the $n$ that will accomplish that, you need to know the distribution of $Q$ for your dishonest die.

Then $Q$ has a noncentral chi-squared distribution $Chisq(\nu = 5, \lambda)$, with noncentrality parameter $\lambda.$ Here is how to find $\lambda$ for your dishonest die. The null hypothesis assumes probabilities $p_0 = (1/6, 1/6, 1/6, 1/6, 1/6, 1/6)$ for the six faces. Under the alternative hypothesis that the die is unfair the probabilities are $p_1 = (1/5, 1/5, 1/5, 1/5, 1/5, 0).$ Then $$\lambda = nS = n\sum_{i=1}^6 \frac{(p_{1i} - p_{0i})^2}{p_{0i}}.$$ For your unfair die, $S = 0.2,$ so you have $\lambda = ns = 0.2n.$

 p.0 = rep(1/6, 6)
 p.1 = c(rep(1/5,5),0)
 s = sum((p.1 - p.0)^2/p.0);  s
 ## 0.2

Now you want to know $n$ such that $$P(Q > 11.07 | \nu = 5, \lambda = 0.2n) = .5.$$

This probability is called the power of the test at the 5% level, against the alternative face probabilities $p_1.$

We can find $n$ by computing the power for many values of $n$, and picking the smallest one that makes the power exceed 0.5. The answer is $n = 41$ (when $\lambda = ns = 8.2$) If you were fussier and wanted a 95% chance of detecting your die is dishonest, then you would want $n = 106.$

 n = 30:1000
 pwr = 1 - pchisq(11.0705, 4, .2*n)
 min(n[pwr > .5])
 ## 41
 min(n[pwr > .95])
 ## 106

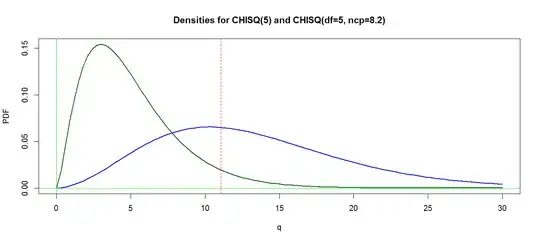
The figure below shows the PDF of the central chi-squared distribution $Chisq(\nu = 5)$ for a fair die (green), and the noncentral chi-squared distribution $Chisq(\nu =5, \lambda=8.2)$ for your dishonest die (blue). You can see that about half the area under the latter curve is to the right of the critical value $q^* = 11.07.$

Reference: The power of the GOF test is not routinely explained in basic statistics courses because it takes specialized software such as R to find probabilities for the noncentral chi-squared distribution. However, you can find an formal explanation in a paper by Guenther (1977) in The American Statistician. (The preview page you can get in Google has the formula for $\lambda.$ He uses detecting an unfair die as one of his examples. If interested, you can probably find a university library with access to the article.)

Note: In your specific case where one of the faces on your unfair die is impossible, you could use the method proposed by @RossMillikan, and get a smaller answer. For $X \sim Binom(4, 1/6),$ one has $P(X = 0) \approx .48.$ [Even quicker, you could likely just look at the die. A typical unfair die might have faces 1, 2, 3 (with a common corner) slightly less likely than 1/6, and faces 4, 5, 6 slightly more likely. This might be done by embedding a lead weight in the plastic just beneath the 123-corner.]