Two tails in a row - what's the probability that the game started with a head?

Question

We're tossing a coin until two heads or two tails in a row occur. The game ended with a tail. What's the probability that it started with a head?

Let's say we denote the game as a sequence of heads and tails, e.g. $(T_1, H_2, T_3, H_5, H_6)$ is a game that started with a tail and ended with a head. In this notation, I need to find $P(H_1 | T_{n-1}T_{n})$.

$$P(H_1 | T_{n-1}T_{n}) = \dfrac{P(H_1 \cap T_{n-1}T_{n})}{P(T_{n-1}T_{n})}$$

For a given $n$, there is exactly one sequence starting with a head and ending with two tails: $(H_1, T_2, H_3, ..., H_{n-2}, T_{n-1}, T_n)$ - this is the event mentioned in the numerator. Now, there are two options for the event in the denominator: either the game is $(H_1, T_2, H_3, ..., H_{n-2}, T_{n-1}, T_n)$, or $(T_1, H_2, T_3, ..., H_{n-2}, T_{n-1}, T_n)$ - they differ in length by 1, though.

How do I calculate their probabilities? I was thinking of calculating discrete probabilities of sequences of length $n$, but since there are two options for the last event, I'm not sure how it'll work.

Answer 1

If I may, there is an easier approach to that problem.

We know the game ended with tails, so we have one of the following states:

$(T, T), (H, T, T), (T, H, T, T), (H, T, H, T, T), (T, H, T, H, T, T), \cdots $

You get the pattern.

Now notice that if you have a sequence of $n $ flips, the probability you got that sequence was $\frac{1}{2^n} $ right? Because the outcome of one flip was not influenced by the other.

Now we can start by infering this: the first sequence does not start with heads and has probability $\frac14$. The sequence afterwards starts with heads and has probability $\frac12\frac14$ i.e. half the probability of occurring when compared to the previous one. Doing this for all pairs of sequences, we see that each tail-starting sequence has double the probability of happening when compared to a heads-starting sequence and this can only happen if the probability of the game starting with tails is $66\% $ and with heads is $33\% $.

Another way of doing this is by explicitly summing all the probabilities of all sequences that start with heads. That sum is

$$\sum_{i = 1}^{\infty} \frac{1}{2^{2i + 1}} = \frac16$$

This is $P(\text{starts with heads|ends with tails}) $. Now all we have to do is divide by the probability it ended with double tails, since that is already given, to get $P(\text{starts with heads})$. The probability it ended with double tails is given by summing the probabilities of all these sequences (show it equals $\frac12$).

Now $\frac16/\frac12 = \frac13$ which is the result we obtained intuitively.

Answer 2

Suppose the game ends on the $n$th toss with a tail. If $n$ is even, then the first toss must be tails; if $n$ is odd, then the first toss must be heads. For example, if $n=3$, then the sequence must be $HTT$. If $n=4$, it must be $THTT$. If $n=5$, it must be $HTHTT$. Etc.

\begin{align} P(H_1 | \text{ends with tails}) &= \frac{P(H_1,\text{ends with tails})}{P(\text{ends with tails})}\\ &= \frac{\sum_{n=2}^\infty P(H_1, \text{ends on $n$th toss with tails})}{1/2}\\ &= 2(0 + 2^{-3} + 0 + 2^{-5} + 0 + 2^{-7} + \cdots)\\ &= \frac{1}{4} \cdot \frac{1}{1-(1/4)}\\ &= \frac{1}{3}. \end{align}

Answer 3

You have already made a key observation about the structure of the game. In general, if $x,y \in \{T,H\}$and $x\neq y$ a game will take one of these forms (always ending with two tosses of the same outcome) $$ \begin{array}{rl} \color{red}{x\ x} &\quad 2 \text{-toss sequence} \\ y\ \color{red}{x\ x} &\quad 3 \text{-toss sequence} \\ x\ y\ \color{red}{x\ x} &\quad 4 \text{-toss sequence}\\ y\ x\ y\ \color{red}{x\ x} &\quad 5 \text{-toss sequence}\\ ... &\quad ... \end{array} $$

What is the probability for the first case (length = $2$)? It's $\frac{1}{2}$ (we start with any face and then we have to get the same face). For length =$3$? It's $1 \over 4$ (we start with any face and then we have to get the opposite face twice). For a length 4 sequence we start with any face and then have to get the opposite face and the same face twice (probability $1 \over 8$). In general, the probability of getting a sequence of $n$ tosses is $\frac{1}{2^{n-1}}$. As a quick sanity test, we see that if we sum up the probabilities of the infinite number of cases we get $1$ .

Now notice that we start with the same face as we end for cases of lengths $2,4,6,8,\dots$ and we start with the opposite face when the length is $3,5,7,9,\dots$

The crucial observation is to see that sequences with lengths $2,4,6,\dots$ have double the probability of sequences of length $3,5,7,\dots$

Hence we have double the probability of starting with the same face we end, compared to starting with the opposite face. So:

$$P(H_1|T_n) = \frac{1}{3} \quad \text{and}\quad P(T_1|T_n) = \frac{2}{3}$$

Answer 4

Let $E_H, E_T$ be the events of ending heads or tails, respectively, and $B_H, B_T$ those of beginning such. Let $S,L$ be the events of ending on the second toss or ending later.   Then by the law of total probability:

$$\mathsf P(E_T) = \mathsf P(E_T, B_T, S)+\mathsf P(E_T, B_T, L)+\mathsf P(E_T,B_H)$$

We note by symmetry that the unconditional probability of ending on two heads is the same as the unconditional probability of ending on two tails, which must mean:

$$\mathsf P(E_T) = \tfrac 12$$

To begin with a tail and end with a tail on the second toss, requires tossing two tails, obviously, so

$$\mathsf P(E_T,B_T,S)=\tfrac 14$$

To begin with a tail and end with a tail later than the second toss, requires tossing a tail then ending with a tail after restarting with a head.

$$\mathsf P(E_T, B_T, L)= \tfrac 12\mathsf P(E_T, B_H)$$

Put it all together to find $$\mathsf P(B_H\mid E_T)=\frac{\mathsf P(E_T, B_H)}{\mathsf P(E_T)}$$

Answer 5

For problems like this, I usually find that it's way easier to graph out the state of the game first, before you attempt to tackle it:

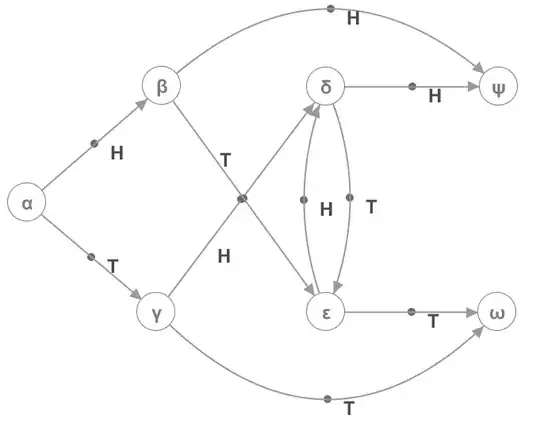
Frustratingly I can't find any decent graph plotting software, but it works like this. Start at node $\alpha$. Each time you flip a coin, look at the edge labelled with that face and follow it to the next node. Keep going until you reach either $\psi$ or $\omega$. Following this graph is identical to playing this game. If you ever toss two consecutive heads, you'll end up in $\psi$. If you ever toss two consecutive tails, you'll end up in $\omega$. If the first toss is a head we'll visit $\beta$ and if the first toss is a tail we'll visit $\gamma$. If the tosses alternate we'll flip-flop between $\delta$ and $\varepsilon$ until we eventually escape. Take a moment to sit and figure out the graph, and possibly draw a better one in your notebook, before you attempt to do anything else with it.

Let $\tilde{\beta}$ be the event that we visit node $\beta$ at some point whilst playing the game. Let $\tilde{\omega}$ be the event that visit $\omega$ at some point. We're now trying to find $\mathbb{P}(\tilde{\beta}|\tilde{\omega})$. A quick Bayesian flip gives us

$$ \mathbb{P}(\tilde{\beta}|\tilde{\omega}) = \frac{\mathbb{P}(\tilde{\omega}|\tilde{\beta})\mathbb{P}(\tilde{\beta})}{\mathbb{P}(\tilde{\omega})} $$

It's pretty clear that $\mathbb{P}(\tilde{\beta})=\frac{1}{2}$, since the only way for that to happen is for us to get a head on our first throw.

Noting that the coin is fair and the labels "head" and "tail" are completely arbitrary, the probability that we ever reach $\psi$ must equal the probability we ever reach $\omega$. Though I'll leave the proof out, we're guaranteed to eventually reach one of the two, so we must have that $\mathbb{P}(\tilde{\omega})=\frac{1}{2}$, too.

The two halves cancel, so this leaves us with the result that $\mathbb{P}(\tilde{\beta}|\tilde{\omega}) = \mathbb{P}(\tilde{\omega}|\tilde{\beta})$

Let $\alpha, \beta, \gamma, \delta, \epsilon$ be the events that we are currently in the relevant state. Because there's no way back to $\beta$ after leaving it, we have that $\mathbb{P}(\tilde{\omega}|\tilde{\beta})$ is precisely the probability that we eventually reach $\omega$ given that we're currently at $\beta$. Partitioning over transitions out of $\beta$, we have that $\mathbb{P}(\tilde{\omega}|\beta) = \frac{1}{2}(\mathbb{P}(\tilde{\omega}|\psi) + \mathbb{P}(\tilde{\omega}|\varepsilon)) = \frac{1}{2}\mathbb{P}(\tilde{\omega}|\varepsilon)$.

Now, $\mathbb{P}(\tilde{\omega}|\varepsilon) = \frac{1}{2}(\mathbb{P}(\tilde{\omega}|\omega) + \mathbb{P}(\tilde{\omega}|\delta)) = \frac{1}{2} + \frac{1}{2}\mathbb{P}(\tilde{\omega}|\delta)$

Also, by similar logic, $\mathbb{P}(\tilde{\omega}|\delta) = \frac{1}{2}\mathbb{P}(\tilde{\omega}|\varepsilon)$

Plugging these two equalities into each other, we get $\mathbb{P}(\tilde{\omega}|\varepsilon) = \frac{2}{3}$, and so $\mathbb{P}(\tilde{\omega}|\tilde{\beta}) = \frac{1}{3}$

If you're interested, these sorts of things are called Markov Chains, and they're really useful for these sorts of "constantly do random things in sequence" type questions.