13

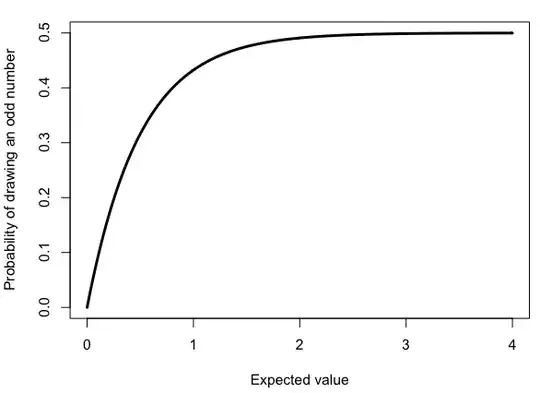
Below is a graph showing the probability of drawing an odd number (y-axis) from a Poisson distribution with a given expected value (x-axis)

x = seq(0,1e4,1)         // range of values to explore 
lambdas = seq(0,4,0.01)  // expected value of the Poison distribution

FracOdd = numeric(n+1)       // response variable
for (i in 1:length(lambdas)) 
{
   FracOdd[i] = sum(dpois(x,lambdas[i])[seq(2,length(x),2)])  // calculate probability of drawing an odd number
}

plot(y=FracOdd,x=lambdas, type="l", lwd=3, xlab="Expected value", ylab="Probability of drawing an odd number")   // plot the data

enter image description here

It seems that the probability of drawing an odd number from a Poisson distribution with non-infinite mean is always lower than the probability of drawing an even number.

  • What is the intuition for why the probability of drawing an odd number from a Poisson distribution always below 0.5?
  • Is the function I drew numerically, easy to derive analytically?
Remi.b
  • 1,655
  • Have you tried computing the probability analytically? I guess you will easily get $\frac{1}{2}(1-e^{-2\lambda})$ for odd draws of Poisson distribution of rate $\lambda$. – Sangchul Lee Nov 09 '16 at 23:37

2 Answers2

16

$\newcommand{\bbx}[1]{\,\bbox[8px,border:1px groove navy]{{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ \begin{align} &\bbox[5px,#ffd]{\sum_{n = 0}^{\infty}{\expo{-\lambda}\lambda^{2n} \over \pars{2n}!}} = \expo{-\lambda}\sum_{n = 0}^{\infty}{\lambda^{n} \over n!}\,{1 + \pars{-1}^{n} \over 2} \\[5mm] = &\ {1 \over 2}\,\expo{-\lambda}\ \underbrace{\sum_{n = 0}^{\infty}{\lambda^{n} \over n!}}_{\ds{\expo{\lambda}}}\ +\ {1 \over 2}\,\expo{-\lambda}\ \underbrace{\sum_{n = 0}^{\infty}{\pars{-\lambda}^{n} \over n!}}_{\expo{-\lambda}} \\[5mm] = &\ \bbx{1 + \expo{-2\lambda}\over 2} \\ & \end{align}

Felix Marin
  • 94,079
9

Yeah, it's reasonably well known.

$$\begin{align}\mathsf P(\text{Even}) ~&=~ \sum_{k=0}^\infty \dfrac{\lambda^{2k} e^{-\lambda}}{(2k)!}\\[1ex] ~&=~ e^{-\lambda}\cosh(\lambda)\\[1ex] ~&=~ e^{-\lambda}\tfrac 12(e^{\lambda}+e^{-\lambda})\\[1ex]~&=~ \tfrac12(1+e^{-2\lambda}) \\[2ex]\mathsf P(\text{Odd}) ~&=~ \sum_{k=0}^\infty \dfrac{\lambda^{2k+1} e^{-\lambda}}{(2k+1)!} \\[1ex]~&=~ e^{-\lambda}\sinh(\lambda)\\[1ex] ~&=~ e^{-\lambda}\tfrac 12(e^{\lambda}-e^{-\lambda})\\[1ex]~&=~ \tfrac12(1-e^{-2\lambda})\\[2ex]e^{-\lambda}(\cosh\lambda-\sinh\lambda)~&=~e^{-2\lambda}\end{align}$$

Graham Kemp
  • 133,231