Differentiablity of the function $\min\{|x-2|,|x|,|x+2|\}.$

Question

How to check differentiablity of the function $\min\{|x-2|,|x|,|x+2|\}?$ I only know that inside functions are not differentiable at $2,0,-2$ resp. Please help. Thanks a lot.

Use the axioms of an ordered field to check where is $\min$ in each case for any partition of $\Bbb R$. — , Oct 22 '16 at 07:33
Me: "Draw its graph." OP: "i want mathematically solution..." Sure, we got that, but why should this fact prevent you from drawing a graph of the function? If you had followed my suggestion, the solution would have become obvious and you could have transformed what you would have seen on the graph into a full mathematical proof. Next time, you might want to try to understand suggestions before discarding them... — Did, Oct 22 '16 at 07:52
@Macroso Don't you think that "the axioms of an ordered field" is at 30000 feet above the mathematical level of neelkanth who is due to be ending his high school ? — Jean Marie, Oct 22 '16 at 08:37
This is very similar function to the one given in this famous answer. — Martin Sleziak, Oct 22 '16 at 10:23

score 3 · Answer 1 · answered Oct 22 '16 at 07:32

3

Hint: Graph it! Here is the piecewise of this function

$$ f(x) = \begin{cases} -2 -x, \; \; \; x<-2 \\ |x|, \; \; \; -2 \geq x \leq 2 \\ x -2 \; \; \; x > 2 \end{cases} $$

It looks something like this:

    \ \/ /

answered Oct 22 '16 at 07:32

ILoveMath

10,999

Ah, the conceptual graph xD. +1 for the graph art. – Oct 22 '16 at 07:35
1

I am sorry: there are not 3 cases, but 5 cases (see the graphical representation in my answer). – Jean Marie Oct 22 '16 at 07:38
1

I thin you made a mistake, there are changes at -1 and 1 too (you have to split the [-2,2] domain. It looks more like /// – Edouard L. Oct 22 '16 at 07:38
Following your style ILoveMath the graph seems to be something like \/\/\/ – Oct 22 '16 at 07:42
3 cases is not wrong, but something like vvv. – Takahiro Waki Oct 22 '16 at 08:09
@Takahiro Waki I wouldn't like to be too insistant but the answer of ILoveMath is erroneous, and he/she should correct it. – Jean Marie Oct 22 '16 at 08:40

score 3 · Accepted Answer · answered Oct 22 '16 at 07:35

3

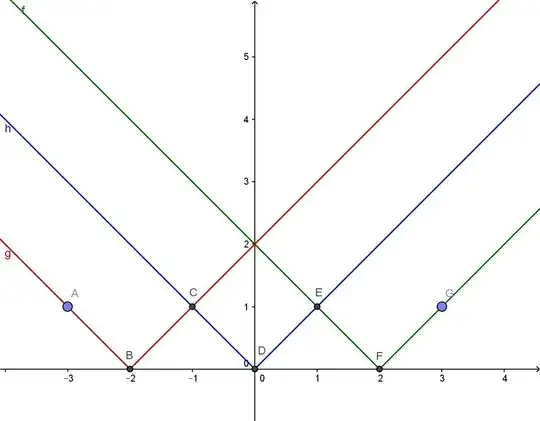
Hint: What is the connection between the broken line ABCDEFG and your problem?

What do you think for example in point B of the left derivative versus the right derivative?

answered Oct 22 '16 at 07:35

Jean Marie

88,997

Edouard L. · Answer 3 · 2016-10-22T07:53:38.073

You can rewrite the function as follows:
1) On $]-\infty,-2], f(x)=f_1(x)=-x-2$
2) On $[-2,-1], f(x)=f_2(x)=x+2$
3) On $[-1,0], f(x)=f_3(x)=-x$
4) On $[0,1], f(x)=f_4(x)=x$
5) On $[1,2], f(x)=f_5(x)=-x+2$
6) On $[2,\infty[, f(x)=f_6(x)=x-2$
On each of the open domains, the function is linear and therefore differentiable.
At each of the "intermediate points" {-2,-1,0,1,2} the function is not differentiable (left and right limit of the derivative are different). For example, $f'_1(x)=-1$ and $f'_2(x)$=1, so that $\lim_{x \to -2^-} f'(x)=-1 \neq \lim_{x \to -2^+} f'(x)=1$

Differentiablity of the function $\min\{|x-2|,|x|,|x+2|\}.$

3 Answers3