When to stop rolling a die in a game where 6 loses everything

Question

You play a game using a standard $6$-sided die. You start with $0$ points. Before every roll, you decide whether you want to continue the game or end it and keep your points. After each roll, if you rolled $6$, then you lose everything and the game ends. Otherwise, add the score from the die to your total points and continue/stop the game. When should one stop playing this game? Obviously, one wants to maximize total score.

As I was asked to show my preliminary results on this one, here they are:

If we simplify the game to getting $0$ on $6$ and $3$ otherwise, we get the following:

$$ EV = \frac{5}{6}3+\frac{25}{36}6+\frac{125}{216}9+\cdots = \sum_{n=1}^{\infty}\left(\frac{5}{6}\right)^n3n $$

which is divergent, so it would make sense to play forever, which makes this similar to the St. Petersburg paradox. Yet I can sense that I'm wrong somewhere!

Answer 1

Before deciding whether to stop or roll, suppose you have a non-negative integer number of points $n$.

How many more rolls should you make to maximise the expected gain over stopping (zero)?

Suppose that further number of rolls is another non-negative integer $k$. Now consider the $6^k$ possible sequences of $k$ rolls:

• In $5^k$ of those sequences there is no six and you win some points. The sum $D_k$ over all such sequences of the sum of dice rolls within each sequence satisfies the recurrence relation $$D_0=0\quad D_{n+1}=5D_n+15\cdot5^n$$ It turns out that this has a closed form: $$D_k=15k\cdot5^{k-1}=3k\cdot5^k$$
• In the remaining $6^k-5^k$ sequences there is at least one six and you lose the $n$ points you had beforehand.

So the expected gain when you have $n$ points and try to roll $k$ more times before stopping is $$G(n,k)=\frac{D_k-n(6^k-5^k)}{6^k}=\frac{3k\cdot5^k-n(6^k-5^k)}{6^k}$$ For a fixed $n$, the $k$ that maximises $G(n,k)$ is $m(n)=\max(5-\lfloor n/3\rfloor,0)$; if $3\mid n$ then $k=m(n)+1$ also forms a maximum.

---

Suppose we fix the maximum number of rolls before starting the game. At $n=0$, $k=5$ and $k=6$ maximise $G(n,k)$ and the expected score with this strategy is $$G(0,5)=\frac{15625}{2592}=6.028163\dots$$ But what if we roll once and then fix the maximum rolls afterwards? If we roll 1 or 2, we roll at most 5 more times; if 3, 4 or 5, 4 more times. The expected score here is higher: $$\frac16(1+G(1,5)+2+G(2,5)+3+G(3,4)+4+G(4,4)+5+G(5,4))=6.068351\dots$$ We will get an even higher expected score if we roll twice and then set the roll limit. This implies that the greedy strategy, outlined below, is optimal:

Before the start of each new roll, calculate $m(n)$. Roll if this is positive and stop if this is zero.

When $n\ge15$, $m(n)=0$. A naïve calculation that formed the previous version of this answer says that rolling once has zero expected gain when $n=15$ and negative expected gain when $n>15$. Together, these suggest that we should stop if and when we have 15 or more points.

Finding a way to calculate the expected score under this "stop-at-15" strategy took quite a while for me to conceptualise and then program, but I managed it in the end; the program is here. The expected score works out to be $$\frac{2893395172951}{470184984576}=6.1537379284\dots$$ So this is the maximum expected score you can achieve.

Answer 2

In the last round you can get $\frac{1+2+3+4+5}{6}$ or lose $p\frac 1 6$, whenever the second is more than the first you should stop. So once you have scored more than 15 you should stop. If you score 15 it doesn't matter if you continue or stop.

Answer 3

The question is missing the concept of utility, a function that specifies how much you value each possible outcome. In the game, the utility of ending the game with a certain score would be the value you place on that outcome. Although you could certainly argue it is implied in the question that the utility of a score is simply the score, I would like to add an answer that takes a non-trivial utility into account. If each point translated to 1000 USD, for example, you might have a utility that looks more like $U(x) = \log(x)$ than $U(x) = x$.

Let's say that $U(x)$ is the utility of score $x$ for $x \ge 0$ and assume that $U$ is monotonically non-decreasing. Then we might say that the optimal strategy is that which maximizes $E[U(X)]$, where $X$ is a random variable representing the final score if one plays with the policy where you roll the die if and only if your current score is less than $t \in \mathbb{Z}_{\ge 0}$. (It is clear that the optimal policy must have this form because the utility is non-decreasing.)

Let $Z$ denote current score. Suppose we are at a point in the game where our current score is $z \ge 0$. Then

$$E[U(X)|Z = z] = \frac{1}{6} \left( U(0) + \sum_{i=1}^5 E[U(X)|Z=z+i] \right) \text{ if } z < t$$

$$E[U(X)|Z = z] = U(z) \text{ if } z \ge t$$

Note that for many choices of $U(x)$ the recurrence relation is very difficult to simplify, and that, in the case of choosing to roll the die, we must consider the expected change in utility from that roll and all future rolls. The figures below are examples of what the above recurrence relation gives for $U(x) = x$ and $U(x) = \log_2(x + 1)$. The expression $E[U(X)]$ means $E[U(X)|Z=0]$, because at the start we have $0$ points. The horizontal axis corresponds to different policies, and the vertical axis corresponds to expected utility under each policy.

Gist with Python code

Answer 4

There is unfortunately many mistakes in the calculation of the expectation proposed:

1) The expectation does not take into account the optionality of the player deciding to play or not.

2) Also since the number of throws is not defined in your calculation and amalgamates all the possible games played (depending on number of throws), the calculation is fundamentally flawed. For example the probabilities you are using do not add up to 1. $$\sum_{i=1}^{\infty} (5/6)^n = \frac{1}{1-5/6} -1= 5 $$

3) You seem to confuse the question as to when you should stop playing and what is the expected value of the bet (whose number of dice throw should be specified)

Now for possible answers, I will keep the simplified setting you have used:

1) One way to have some intuition about the problem is to assume the game consist of $n$ throws and calculate the expected gain of that game denoted $X_n$. Let us also note $I_n$ the indicator that a 6 was NOT rolled on the $n$-th roll, i.e. $I_n=1$ if a 6 is not rolled. The intuition here if that for the game to payout $3j$ with $1\le j\le n$ you need to have $j$ rolls that aren't 6 and an initial roll of 6 before that streak (except if the streak lasts the entire $n$ rolls):

$$ E[X_n] = \sum_{j=1}^{n-1} 3j (5/6)^j (1/6) + 3n(5/6)^n $$

Since this is a bit annoying to solve for in a nice formula one can use conditional expectation to find an induction step: $$E[X_n \mid X_{n-1}] = E[(X_{n-1}+3)I_n \mid X_{n-1}] = (X_{n-1}+3)E[I_n] = \frac{5}{6}(X_{n-1}+3)$$ Note that if your gains are $X_{n-1}$ after $n-1$ rolls that your gains are either 0 if you roll a 6 next (i.e. $I_n=0$) or your gains are $X_{n-1} +3$.

Thus the expectation follows the induction $E[X_n] = \frac{5}{6} (E[X_{n-1}] + 3)$ and starts with $E[X_1] = 3\frac{5}{6} = 2.5$.

Now the expectation increases as $n$ grows towards the limit 15, which you can determine by the equation $l=\frac{5}{6} (l+3)$.

Hence this analysis would suggest the longer you play the better off you are in average. In view of my following point this limit of expectation is very uninformative (slightly like the St. Petersburg paradox).

2) I will make this one short(er). The second Borel-Cantelli lemma implies that if you play forever, you will infinitely often roll a six with probability 1. Hence you will forever return to 0 gain. That is the bad news!

The good news is that the same lemma implies that if you fix a gain target $x$ (if you go above $x$ you stop the game and leave with your gains) and you play infinitely often (or until you reach the target). Then you will hit your target with probability 1 (it might take a very long time unfortunately depending on the target).

These two facts illustrate further how uninformative the expectation is in this situation.

I hope this helps and wasn't too long (well maybe not extremely long at this point...)

Answer 5

I'm going to tackle the problem of trying to maximize the average score of a strategy, with the disclaimer that this is often not what you actually care about when playing actual games.

Often, the trick to the math is to try and express the result algebraically in terms of simpler (and hopefully independent!) random variables.

This can be done here. Suppose you select some strategy, and define:

• $P_n = 0$ if you would stop at a score of $n$, and $P_n = 1$ if you continue.
• $R_n = 1$ if your game ever reaches a state where your score is exactly $n$, and $R_n = 0$ otherwise
• $X_n$ is the change in score you would get from rolling a die at score $n$

i.e. on that last point, $X_n$ would either be $1, 2, 3, 4, 5,$ or $-n$ with equal probability.

Then, your score from playing the game is

$$ S = \sum_{n=0}^{\infty} P_n R_n X_n $$

The most important feature of the sum is that the $X_n$ are independent from all of the other random variables, and thus we can express the expected score, using the two facts:

• $\mathbb{E}(Y+Z) = \mathbb{E}(Y) + \mathbb{E}(Z)$
• $\mathbb{E}(YZ) = \mathbb{E}(Y) \mathbb{E}(Z)$ if $Y$ and $Z$ are independent

to get

$$ \mathbb{E}(S) = \sum_{n=0}^{\infty} \mathbb{E}(P_n R_n) \mathbb{E}(X_n) $$

Since $\mathbb{E}(X_n) = \frac{5}{2} - \frac{n}{6}$, we have

• $\mathbb{E}(X_n) > 0$ if $n < 15$
• $\mathbb{E}(X_n) = 0$ if $n = 15$
• $\mathbb{E}(X_n) < 0$ if $n > 15$

and the formula for the average score is simple enough that it makes it obvious what the optimal strategy is:

• Play whenever the current score is less than 15
• It doesn't matter what you do when the score is exactly 15
• Stop whenever the score is greater than 15

The reason this is optimal is because:

• It maximizes the values of $\mathbb{E}(P_n R_n)$ for all of the terms where $\mathbb{E}(X_n) > 0$, so as to get the greatest contribution from the rolls that would increase your score on average
• It makes $\mathbb{E}(P_n R_n) = 0$ for all of the terms where $\mathbb{E}(X_n) < 0$, so as to eliminate their contribution to the average.

---

If you had a utility function (as suggested in this other answer), you could replace $X_n$ with the change in utility. Depending on the specific form of the utility function, the overall approach may or may not still apply.

Answer 6

It's not hard to see that the optimal strategy in this game is "stop on $k$ or higher," for some positive integer $k$. This is because what is optimal is only determined by your current score, not your history of rolls, and if rolling again on $k$ is unwise, then rolling again on $k+1$ is unwise as well (you stand to gain the same amount from future rolls, but have more to lose).

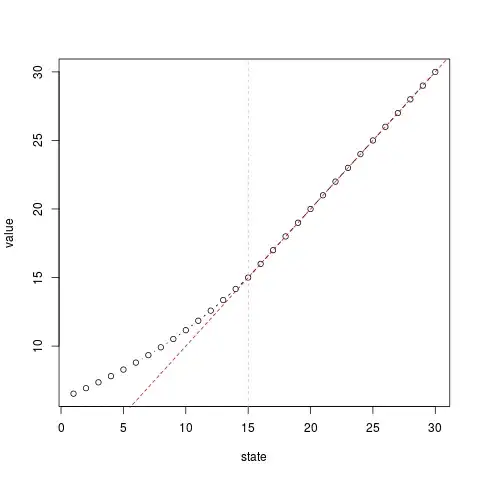
Let's compare the strategies "stop on $k$ or higher" with "stop on $k+1$ or higher". If your score is never $k$, then these strategies result in the same final score. If you do reach $k$, then the first strategy will result in $k$, while the second will result in $\frac56k+\frac16(1+2+3+4+5)$. Comparing these, we see that the stop on $k$ strategy is better precisely when $k>15$, is worse when $k<15$, and you should be indifferent between then two when $k=15$.

---

Here is a proof which is more obviously rigorous. Let $V(k)$ denote the expected gain from future rolls when you play the optimal strategy, starting from a total of $k$. By considering the two options of roll again or stop, we get $$ V(k)=\max\left(0,\frac16\left(\sum_{i=1}^5 (V(k+i)+i)\right)+\frac16(-k)\right) \\=\max\left(0,\frac{15-k}6+\frac16\sum_{i=1}^5V(k+i)\right) $$ We can now prove that $V(k)>0$ if and only if $k<15$. This means that is strictly optimal to roll again if and only if your total score is less than $15$.

Certainly, if $k<15$, then $V(k)\ge \frac{15-k}6+\frac16\sum_{i=1}^5V(k+i)\ge \frac{15-k}6$, because $V(k+i)\ge 0$. We conclude that $V(k)>0$ when $k<15$, as claimed. However, when $k\ge 15$, more care is required.

First of all, I can prove that $$ V(k)\le 15\text{ for all }k.\tag{$*$} $$ To see this, consider a modified game where rolling a six simply stops the game, without taking away your accumulated points. Certainly, this game is more favorable to the player. For the modified game, it is optimal to roll until you get a six, so the expected gain from future rolls is exactly $5\cdot 3$, as you will roll on average $1/(1/6)=6$ times more, and the first five rolls give you three points each on average.

Using $(*)$, you can prove that $V(k)=0$ for all $k\ge 90$, because $$ \frac{15-k}6+\frac16\sum_{i=1}^5V(k+i) \le \frac{15-k}6+\frac16\sum_{i=1}^515 =\frac{90-k}6 \le 0. $$ We can now prove that $V(k)=0$ for the remaining cases $15\le k\le 89$ by reverse induction on $k$. That is, given $k\ge 15$, we assume that $V(\ell)=0$ for all $\ell>k$, and use this to prove $V(k)=0.$ The proof is simple: $$ V(k) =\max\left(0,\frac{15-k}6+\frac16\sum_{i=1}^5V(k+i)\right) =\max\left(0,\frac{15-k}6+0\right)=0. $$

Answer 7

The mathematics of this is actually very simple, every time you roll you have a 1 in 6 chance of losing regardless of previous outcomes so the optimal strategy depends on information not covered by the question and ultimately depends on your ability to judge when your score is adequate.

There are two obvious scenarios here.

Firstly you are playing on your own for some reward, say you get one dollar for every point, here with each roll you are playing the same odds but for an increased stake so it is really down to your own greed/prudence when you stop and cut your losses ie how much are you prepared to lose.

Actually here a sensible strategy is to pick a score to stop at which you consider to be a good return. Obviously in this case there is no upper limit to the maximum score as you could keep rolling not six indefinitely and at every roll the chance of increasing your score is 5/6.

Here at every stage you are betting an increasing stake for the same potential reward.

The other scenario is if you are playing against other players (eg like poker as opposed to horse racing) here is is slightly more complex as you are trying to bluff your opponents. Here it is useful to know your expected score.

If for the sake of simplicity we call 6 zero than the average score per throw is

[0+1+2+3+4+5]/6 = 2.5

So the average score for n throws is 2.5n

So here it becomes a lot like poker, if you 'fold' you are forcing the other players to guess your score and press on or not eg if after 10 throws you have 10 fives you are in a very strong position as you have a score of 50 and the average player has a score of only 25 and needs, on average another 11 successful (non 6) throws to beat you outright on average.

So really this is more about the psychology of risk and there is no well defined optimal strategy without having a specific goal in mind.

You could say though that the only 'best' strategy is to roll once and then quit, if you win your are ahead (assuming no stake) if you lose you've lost nothing.

Answer 8

You should stop when the expected score from another toss becomes negative or zero. Let $X$ be the score; the expected gain for the next toss is: $$ 1/6\times1+1/6\times2+1/6\times3+1/6\times4+1/6\times5+1/6\times(-X)=\frac{15-X}{6}. $$ Therefore you should stop as soon as your total score is 14 or more.

Of course this assumes linear utility and risk-neutrality.

Answer 9

Here's an answer using value function iteration:

Let $v(x)$ denote the value of state $x$. The Bellman equation for this problem is $$v(x) = \max\left\{u(x), \frac{1}{6} \left[u(0) + \sum^5_{k=1}v(x+k)\right]\right\},$$ where $u$ is the utility of ending the game with $x$.

Several of the answers above point out that the optimal strategy must be "keep gambling until $x \geq x^\star$, then stop", and solve for $x^\star$ analytically.

Here's some R code that solves for $v$ (under linear utility) using value function iteration, i.e. by starting with an incorrect guess for $v$ and then iterating on the Bellman equation until convergence:

## State x is number of points
## Each time period, either stop and enjoy utility u(X), or roll a six-sided die
## If roll a 6, lose everything, game ends, get u(0)
## If roll k < 6, move to state x' = x + k

max_x <- 30  # Maximum state to keep things simple -- in "true" problem this is infinite
value <- rep(0, max_x)

utility <- function(x) {
    return(x)  # Linear utility function
}

n_iterations <- 100  # Value function iteration
for(iteration in seq_len(n_iterations)) {
    value_next <- value
    for(x in seq_along(value)) {
        x_next_if_roll <- pmin(x + seq_len(5), max_x)  # Next period's states if roll 1, 2, ... , 5
        value_next[x] <- max(utility(x), (1/6) * (utility(0) + sum(value[x_next_if_roll])))
    }
    distance <- mean(abs(value - value_next))
    value <- value_next
    message("iteration ", iteration, " value function distance ", round(distance, 4))
    if(distance < 10^-8) break
}

max(which(value > seq_along(value)))  # Last index at which it is optimal to keep playing

plot(value, type="b", xlab="state", ylab="value")
abline(a=0, b=1, lty=2, col="red")
abline(v=max(which(value > seq_along(value))) + 1, lty=2, col="grey")  # Stop when reach this state

sum(value[1:5]) / 6  # Value before starting game (i.e. starting from state x=0): around 6.1537

The value function $v(x)$ when $u(x) = x$:

When $v(x) = u(x)$ (i.e. when you reach a score greater than or equal to 15, the vertical line in the plot above), the optimal action is to stop playing and "consume" your $x$.

Answer 10

I interpreted this such that you're in competition against another player.

If playing second your strategy is simple - play until you've won.

If playing first, you must accumulate enough points such that the next player is statistically more likely to lose than win - that means making them roll more than 6 times (since they have a 1/6 chance of losing every roll). To achieve this you must amass at least the value of the average scoring roll (3) multiplied by 6, which is 18. Any score above this is statistically more likely to win than lose.

Answer 11

Why is your summation divergent? For n sufficiently large, each term is less than 123456 * (11/12)^n, which certainly converges to something finite. Particularly, look up "gradient series" in a book on engineering economics (time value of money). There you will find that x/(1-x)^2 = x+2x^+3x^3+4x^4+... Or you can get it by differentiating both sides of 1/(1-x) = Sum(i=0 to infinity)(x^i). This would seem to indicate that your summation adds up to 90. Of course, selecting a strategy that maximizes your EXPECTED payoff is no guarantee of success on any single game, but it is the best you can do if you play thousands of games.