6

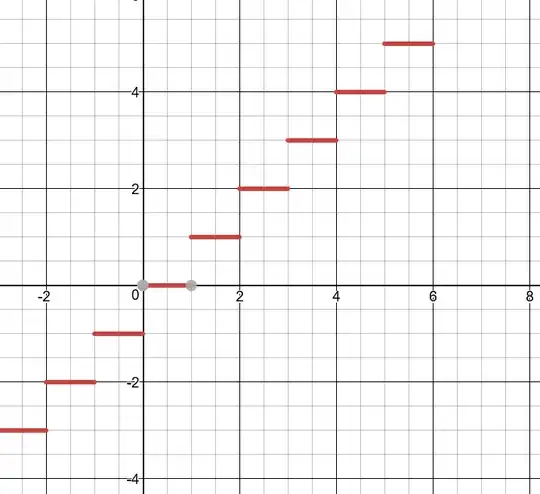
A continuous function is a function where the limit exists everywhere, and the function at those points is defined to be the same as the limit.

I was looking at the image of a piecewise continuous function on the following page: http://tutorial.math.lamar.edu/Classes/DE/LaplaceDefinition.aspx But the image of the function they've presented isn't continuous. As such, I'm confused by what a piecewise continuous function is and the difference between it and a normal continuous function.

I'd appreciate it if someone could explain the difference between a continuous function and a piecewise continuous function. Also, please reference the image of the piecewise continuous function presented on this page http://tutorial.math.lamar.edu/Classes/DE/LaplaceDefinition.aspx .

Thank you.

The Pointer
  • 4,686

4 Answers4

18

A piecewise continuous function doesn't have to be continuous at finitely many points in a finite interval, so long as you can split the function into subintervals such that each interval is continuous.

A nice piecewise continuous function is the floor function:

enter image description here

The function itself is not continuous, but each little segment is in itself continuous.

Simply Beautiful Art
  • 76,603
  • Thank you for the illustration. This makes sense. – The Pointer Oct 14 '16 at 23:44
  • Not OP, but I want to clarification on this point: the floor function looks like it would be discontinuous at an infinite number of points. If the definition of a piecewise continuous function is "doesn't have to be continuous at finitely many points" wouldn't the floor function not satisfy that definition. – Dargscisyhp Oct 14 '16 at 23:45
  • @ThePointer Pleasure. Pictures are great. – Simply Beautiful Art Oct 14 '16 at 23:45
  • 1
    As an aside (not necessarily useful): I imagine we could have countably many discontinuity points also by having a discontinuity point at each natural: like $f(x)=\sum_{n=1}^\infty n\chi_{[n,n+1)}$. – Alekos Robotis Oct 14 '16 at 23:45
  • 1
    @Dargscisyhp Sure, but I guess I would change it to countably infinite then. – Simply Beautiful Art Oct 14 '16 at 23:46
  • That's what I figured, I just wanted to make sure. Thank you. – Dargscisyhp Oct 14 '16 at 23:47
  • 2
    Indeed. And if countably many discontinuities are allowed, then the function that's $1/n$ on the interval $(1/(n+1), 1/n]$ for each positive integer $n$, and $-1/n$ on $[1/n, 1/(n+1) )$ for each negative integer $n$, and is zero at zero...that has infinitely many discontinuities, but they "gather" at 0, which may be a problem for some uses of "piecewise continuous". – John Hughes Oct 14 '16 at 23:47
  • 2
    @JohnHughes Right. Let me fix this to so finitely many points of discontinuity over a finite interval. – Simply Beautiful Art Oct 14 '16 at 23:48
  • 1
    You might also want to require that there are only finitely many in a neighborhood of infinity (which would rule out "floor") in the event that you want to work on the Riemann sphere or something...but that's probably painting the lily. – John Hughes Oct 14 '16 at 23:53
  • @JohnHughes Yeah, that's probably not helpful to the OP at that point XD – Simply Beautiful Art Oct 14 '16 at 23:55
  • 2
    This conversation went 0-100 real quick. I'm just going to thank @SimpleArt for the explanation and move on. – The Pointer Oct 15 '16 at 01:01
  • "...so long as you can split the function into subintervals such that each interval is continuous." This is an important and somewhat subtle point! The function $\sin 1/x$ isn't piecewise continuous even though its only point of discontinuity is $x=0$, because it isn't continuous on the interval $(0,\infty)$. A necessary condition is that the left- and right-hand limits of the function exist at each point. – Carmeister Oct 15 '16 at 03:12
16

A function $f$ is piecewise continuous on an interval $J\subset{\mathbb R}$ if it is continuous apart from a set of isolated points $\xi\in J$ where only the one-sided limits $\lim_{x\to\xi-}f(x)$ and $\lim_{x\to\xi+} f(x)$ exist.

Note that $f(x):=\sin{1\over x}$ $(x\ne0)$ together with $f(0):=0$ does not define a piecewise continuous function on ${\mathbb R}$, even though this $f$ is continuous in the "segments" created by the special point.

Christian Blatter
  • 232,144
  • Could the set of isolated points be null? So all continuous functions (on interval $J$) are automatically ``piecewise continuous"? – welshman500 Apr 17 '19 at 03:43
4

$\newcommand{\R}{\mathbb{R}}$The notion of piecewise continuity (PWC) is used differently in different contexts. a Often, a function $f:\R\to\R$ is called PWC if it continuous everywhere, but at a finite number of points.

In the context of Laplace transform and other integral transforms, a function $f$ is said to be PWC if it is continuous on a partition of intervals of its domain and at the boundaries of the intervals the function has well-defined and finite limits.

Definition. [PWC] A function $f:[a,b]\to\R$ is called piecewise continuous (PWC) if there exist $a = x_0 < x_1 < \ldots < x_n = b$ so that

  1. $f$ is continuous on $(x_k, x_{k+1})$ for all $k=0,\ldots, n-1$
  2. The limits $\lim_{x\to{}x_{k+1}^{-}}f(x)$ and $\lim_{x\to{}x_{k}^{+}}f(x)$ exist and are finite for all $k=0,\ldots, n-1$

According to this definition, function $$ f(x) = \begin{cases} 0, &\text{ for } x = 0 \\ \frac{1}{x}, &\text{ for } x{}>{}0 \end{cases} $$ defined over $[0, \infty)$, is not PWC according to the second definition although it has only one point of discontinuity.

Additionally, function $f(x)=\tfrac{1}{x}$, $x\in\R\setminus\{0\}$, is not PWC, again because the limits $\lim_{x\to 0^+}f(x)$ and $\lim_{x\to 0^-}f(x)$ are not finite.

Pantelis Sopasakis
  • 5,349
0

A piece-wise continuous function is a bounded function that is allowed to only contain jump discontinuities and fixable discontinuities. These functions almost always occur with the inclusion of floor into the regular set of algebraic functions you are used to in calculus. The reason for this is because up until then there are no functions you have encountered containing any form of jump discontinuity of the finite nature. As the other answer here says, each interval is continuous. This is true. However there are levels of piece-wise continuity which simply put mean that the function is differentiatable fully on those continuous intervals n number of times.

user64742
  • 2,195