How to find the area in red?

Question

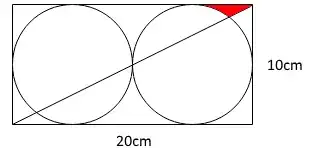
My nephew asked me how to find the area of the red section on this diagram (though he didn't say why). After some head scratching I have to admit the question beat me and now I need to know how it would be calculated to satisfy my own curiosity.

Answer 1

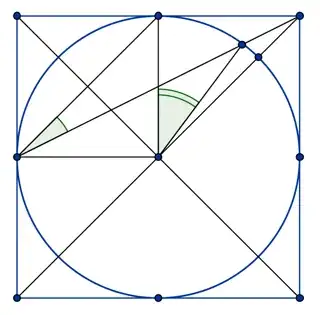
Let $\alpha$ be the single-slanted angle and $\beta=2\alpha$ the double-slanted angle. We have $$\alpha=\arctan(2)-\frac{\pi}{4}=\arctan\frac{1}{3},\quad \beta=2\arctan\frac{1}{3}=\arctan\frac{3}{4}$$ The area of the red region can be computed by sutracting from $\frac{25}{2}$ (that is the area of a isosceles right triangle with leg lengths $5$) the area of the circle sector subtended by $\beta$ and the area of the small triangle having two sides with lenghts $5$, $5\sqrt{2}$ and the angle between them being equal to $$ \gamma=\frac{\pi}{4}-\beta = \arctan\frac{1}{7}.$$ Summarizing, $$\color{red}{A}=\frac{25}{2}-\frac{25}{2}\arctan\frac{3}{4}-\frac{25}{\sqrt{2}}\sin\arctan\frac{1}{7}\approx \color{red}{1.95623614}.$$

Answer 2

Let $A$ be the shaded area and $B$ the area of the unshaded part of the corner. Since one circle of radius $5$ along with the $4$ corners make up a square of area $100$, we have $$4(A+B)+25\pi=100.$$

Let $(0,0)$ be the left bottom vertex of the rectangle. The first circle has equation $(x-5)^{2}+(y-5)^{2}=25$, and the diagonal line is $y=\frac{1}{2}x$. Those intersect in $(2,1)$ and $(10,5)$. Hence, the length of the part of the diagonal line within one circle is $\sqrt{80}$. Now consider the triangle with vertices the center of the first circle, and the points of intersection of the first circle with the diagonal line. By the law of cosines, it has top angle $\alpha\approx 2.21$.

Hence the area of the circle segment below the diagonal is $$\frac{25}{2}(\alpha-\sin\alpha):=C\approx 17.68.$$

Now, consider the triangle with vertices $(0,0), (10,0)$ and $(10,5)$. Computing its area, we get $$25=C+A+A+B,$$ where $C$ is known. Solving the system \begin{cases} 4(A+B)+25\pi=100\\ 25=C+A+A+B \end{cases} gives $A\approx 1.95$.

Answer 3

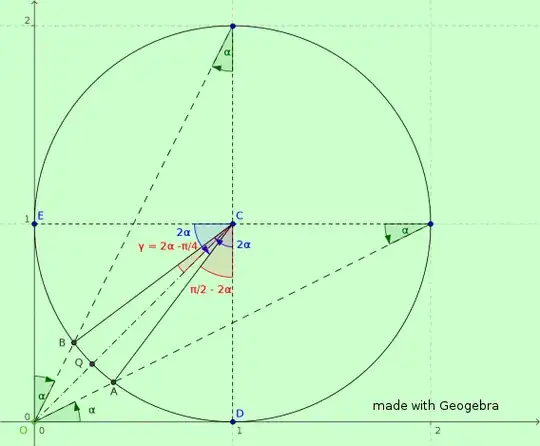
Let me present another approach, making use of the relation between the angles seen from the center and from a point on the circumference.

With reference to the drawing, for a circle of unitary radius we have: $$ \begin{gathered} \alpha = \arctan (1/2) \hfill \\ \gamma = 2\alpha - \pi /4 \hfill \\ \text{Area}_{\;{\Delta }\,\text{OCD}} = 1/2 \hfill \\ \text{Area}_{\;{\Delta }\,\text{OAC}} = \sqrt 2 /2\sin \gamma \hfill \\ \text{Area}_{\;\text{circ}\text{.}\,\text{sect}\text{.}\,\,ACD} = \frac{{\pi /2 - 2\alpha }} {{2\pi }}\pi = \pi /4 - \alpha \hfill \\ \end{gathered} $$ Then it is clear from the drawing that $$ \begin{gathered} \text{Area}_{\;\text{Lun}\text{.}\,\,OAD} = \text{Area}_{\;\text{\Delta }\,\text{OCD}} - \text{Area}_{\;\text{\Delta }\,\text{OAC}} - \text{Area}_{\;\text{circ}\text{.}\,\text{sect}\text{.}\,\,ACD} = \hfill \\ = 1/2 - \sqrt 2 /2\sin \gamma - \pi /4 + \alpha = \hfill \\ = 1/2 - \frac{{\sqrt 2 }} {2}\frac{{\sqrt 2 }} {2}\left( {\sin \left( {2\alpha } \right) - \cos \left( {2\alpha } \right)} \right) - \pi /4 + \alpha = \hfill \\ = 1/2 - \frac{1} {2}\cos ^{\,2} \alpha \left( {\tan ^{\,2} \alpha + 2\tan \alpha - 1} \right) - \pi /4 + \alpha = \hfill \\ = 1/2 - \frac{1} {2}\frac{4} {5}\frac{1} {4} - \pi /4 + \alpha = \hfill \\ = \frac{2} {5} - \pi /4 + \arctan (1/2) \hfill \\ \end{gathered} $$ and, for a circle of radius $5$ we will have: $$ 5^{\,2} \text{Area}_{\;\text{Lun}\text{.}\,\,OAD} = 1.956236.. $$ which matches with the result provided by Jack D'Aurizio