6

I accidentally noticed that:

$$(7)_4=7 \cdot 8 \cdot 9 \cdot 10=2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7=7!$$

Here $(n)_k$ is the Pochhammer symbol.

I wonder, are there any other non-trivial integer solutions $(n,k)$?

$$(n)_k=n!$$

Among the ones I consider trivial we have $(0,0),(1,0),(1,1),(2,1)$. Somehow, I'm sure that I will get a lot of comments with these four solutions.

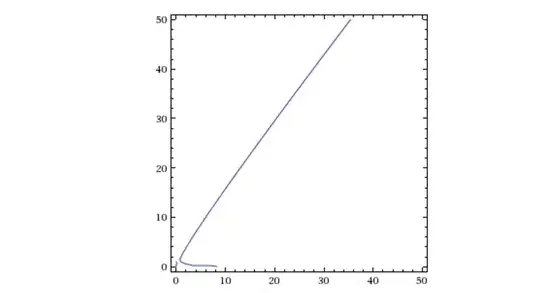
This is the implicit plot of the equivalent equation:

$$\Gamma (n+k)=n \Gamma^2 (n)$$

enter image description here

Community
  • 1
Yuriy S
  • 32,728
  • Nice question... – barak manos Sep 01 '16 at 08:41
  • I wish you the best of luck on this one. – Axoren Sep 01 '16 at 08:44
  • @Axoren, is the problem unsolved? If it is, I'm sure there are reasons... – Yuriy S Sep 01 '16 at 08:46
  • I think that the answer (no) lies in the fact that there is no number larger than $10$ which can be "split" into two parts containing the same prime factors, i.e., there will always be a prime factor which is present in one of the parts but not in the other. In your example, $10$ is "split" into $[1-7]$ and $[7-10]$, both parts containing the same prime factors (and even with the same multiplicity for each factor). – barak manos Sep 01 '16 at 08:47
  • You can easily prove that, if $n>1$, then $n$ must be prime. – Batominovski Sep 01 '16 at 08:56

1 Answers1

3

If $n+k\geq 14$, then there are at two primes in the interval $\left(\frac{n+k-1}{2},n+k-1\right]$. Therefore, $(n+k-1)!$ cannot equal $n\cdot \big((n-1)!\big)^2$. This leaves the cases $n+k\leq 13$ to be dealt with.

Batominovski
  • 50,341