There seems to be no way to get these expressions from both the methods to match. I know the arbitrary constant could vary in different methods but even the strcture of both these expressions are not close to same.
I know there is no calculation error because I differentiated the final expressions in both the methods to get the starting integrand.
Please tell me why the expressions don't match then.
$$\frac15\tan\left({\frac{x-\tan^{-1}\frac34}{2}}\right)=\frac{1}{5}\left(\frac{3\tan\frac{x}{2} -1}{3+\tan\frac{x}{2}}\right)=\frac15\left(\frac{3\tan\frac{x}{2} +9 -10}{3+\tan\frac{x}{2}}\right)$$ $$=\frac35 +\frac{-2}{\tan\frac{x}{2} +3}$$
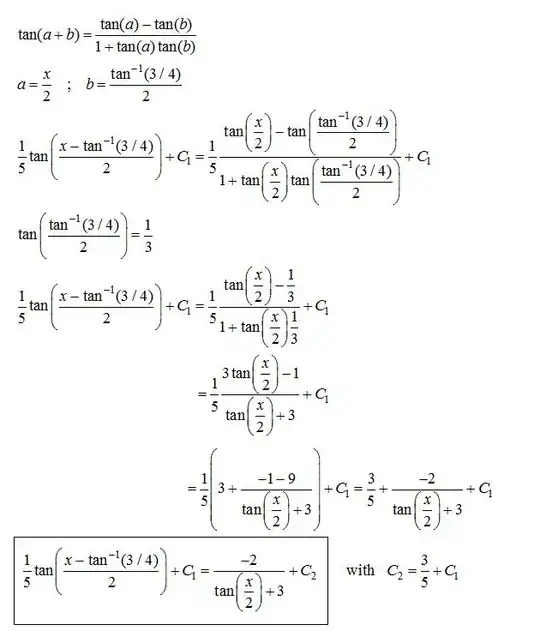
It's hard to tell where you made an error if you don't show your working, your result, or even the problem you're trying to solve.
But that said, I do know a lot of people have trouble seeing "the constants of integration are just different" when it's not directly obvious. For example, they would have trouble recognizing that both solutions
$$ \sin^2 x + C_1 \qquad \qquad -\cos^2 x + C_2 $$
are the same solution, because they did not think to check beyond simply adding a number to the formal expression.
If you really think you have two equal results, consider it a new math problem to see if the two results are the same or different. e.g. do one of the following two things:
Solve for the constant $A$ in $\sin^2 x + A = -\cos^2 x$
to see that they really are equal, or
Find two values $a$ and $b$ so that $(\sin^2 a) - (-\cos^2 a) \neq (\sin^2 b) - (-\cos^2 b)$ have different values.
to see that they really aren't equal. (and so there really must be some mistake or oversight)
