36

I knew from Mark Newman's book - Networks: An Introduction (Page 137, Eq: 6.31) that, if $A$ is the adjacency matrix of a graph, then $ij$'th entry of $A^k$ will give me the number of $k$-length paths connecting the vertices $i$ and $j$. This works very well for directed graphs. But does it work for undirected graphs too?

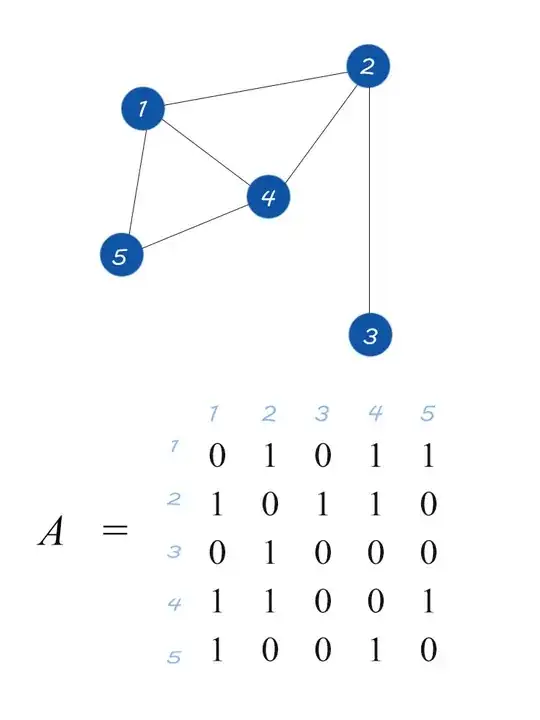
For instance, for the undireceted network below: enter image description here

if i want to calculate how many $3$-length paths are there from vertex-$2$ to vertex-$1$, then I should find $[A^3]_{12}$. Proceeding in this way, I get, \begin{eqnarray} A^3 = \left( \begin{matrix} 4 && 6 && 1 && 5 && 5 \\ 6 && 2 && 3 && 6 && 2 \\ 1 && 3 && 0 && 1 && 2 \\ 5 && 6 && 1 && 4 && 5 \\ 5 && 2 && 2 && 5 && 2 \end{matrix} \right) \end{eqnarray} And, I find,

the entry of the 1st row and 2nd column = 6 = entry of the 2nd row and 1st column.

Does it mean that there are 6 paths of length 3 from vertex-2 to vertex-1? Cearly it is not true because I have only $1$ path of length $3$ from 2 to 1, namely the sequence: $(2,4,5,1)$.

What am I missing?

UPDATE: I am attaching a snapshot of Newman's book. He only talks about "paths", but never about a "walk". Is it a mistake?

Newman's book snapshot

Rodrigo de Azevedo
  • 23,223
kada mati
  • 463
  • 1
    Walk is rather standard in modern graph theory ( Diestel) and path means no edge repetition ( if loops are possible at some vertex then using a loop in the path repeat the vertex once) . Yet at start of paragraph 6.10 Path: Newman mention that 'In general a path can intersect itself' so he uses it as a walk in standard sense. – Jérôme JEAN-CHARLES Apr 28 '20 at 15:14
  • While the existing answers clarified the terminology between path and walk, I am hoping for an answer for (actual) paths. Let's say I make a hack, I always reset the diagonal to zero after each power $A^k = A^{k-1} A$, $ \text{Diag}(A^k) := 0 $ to ban repeated vertices. Would it work? – Moobie Mar 15 '23 at 20:16

2 Answers2

26

The powers of the adjacency matrix don't give you the number of paths but the number of walks between any two vertices. In other words, you need to consider walks such that some vertices/edges are repeated (which do exist).

benguin
  • 3,892
  • 3
    Hi, Thanks for the quick reply, but I think, Newman's book says, it calculates the paths, not walks. I am still confused. :-/ I added a snapshot in the updated question. – kada mati Aug 13 '16 at 00:01
  • How does your book define "path"? – benguin Aug 13 '16 at 01:10
  • 2
    Ahh, got it. They defined "Hamiltonian Path" as the path where a vertex cannot be visited more than once, and "Eulerian path" as the path where an edge cannot be visited more than once. I think, what you meant by "walk" is phrased simply as a "path" in that book. That clears the confusion. Thanks! – kada mati Aug 13 '16 at 02:05
  • 3
    No problem; sometimes different books have subtle differences with regards to terminology, notation, and definitions, graph theory in particular.

    Anyways, with that said, it's not too hard to see the 6 different walks (or paths as per your book) : $(2, 4, 5, 1), (2, 1, 2, 1), (2, 1, 4, 1), (2, 1, 5, 1), (2, 4, 2, 1), (2, 5, 2, 1)$.

     – benguin Aug 13 '16 at 02:55
  • @benguin: Just to understand it completely: should your last mentioned path be (2,3,2,1) instead of (2,5,2,1)? – maze_p Nov 30 '21 at 10:27
  • @maze_p: yes, correct – benguin Dec 01 '21 at 12:37
4

You get the number of $k$ length walks. The difference between a path and a walk is that walks can repeat edges and vertices.

Asinomás
  • 107,565
  • Hi, Thanks for the quick reply, but I think, Newman's book says, it calculates the paths, not walks. I am still confused. :-/ I added a snapshot in the updated question. – kada mati Aug 13 '16 at 00:01
  • Remark: Saying "repeating edges and vertices" is confusing it implicitly says that you could repeat a vertex without repaeating and edge on simple graphs without loops it is impossible. – Jérôme JEAN-CHARLES Apr 28 '20 at 15:01