5

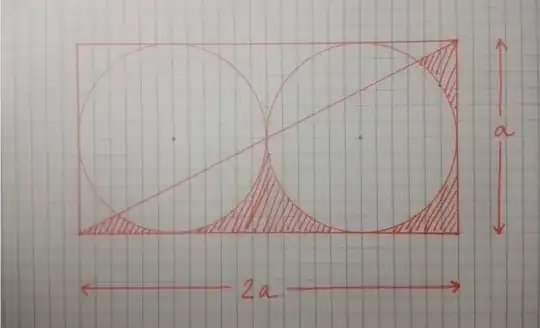
Consider two circles with a diameter equal to $a$, externally tangent to each other, and whose centers are at the same height. Those circles are inscribed inside a rectangle of length $2a$ and height $a$. This is a sketch I made for this problem (please, forgive my unsteady handwriting):

Circles-Inscribed-Inside-Rectangle

I am asked to calculate the shaded area. I can do it using:

  • Symmetry. This is the easiest way in my opinion, since we know the area of each circle ($\pi a^2/4$) and the area of the rectangle ($2a^2$), which gives us: $\boxed{A_{\text{shaded}}=\dfrac{4-\pi}{4} a^2}$
  • Mathematical functions. We can set the origin at the bottom left corner, calculate each of the circles' analytical functions (as well as that of the line), compute the intersections, and make use of definite integrals to compute the final area. It will yield the exact same result as the above, yet the process to achieve it would be much longer.

However, I'm not interested in any of these 2 methods (as they look pretty easy). I'm interested in finding a pure geometrical way to solve it. No functions. No symmetry as I used above. But pure geometric relationships.

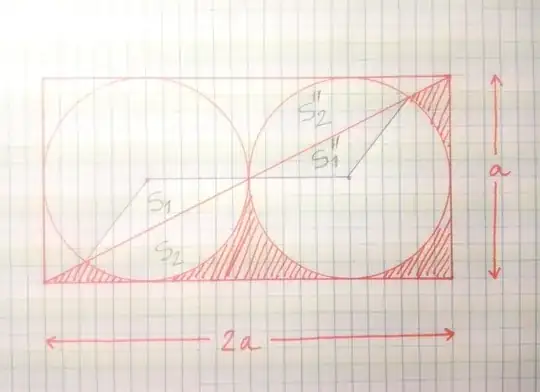
I thought about drawing some lines from the center of each circle to each intersection, like this:

Attempt-P1

This would give us 4 areas hopefully easy to solve for ($S_1$, $S_1^{\prime\prime}$ and $S_2$, $S_2^{\prime\prime}$). Of course, $S_1=S_1^{\prime\prime}$ and $S_2=S_2^{\prime\prime}$ but as I said, I don't want to make use of symmetry (I'm a bit masochistic after all). So I thought about this solving scheme:

  1. $A_{\text{shaded}}=\frac12A_{\text{rectangle}}-S_2-(A_{\text{circle}}-S_2^{\prime\prime})$
  2. $A_{\text{sector}}=S_1+S_2$
  3. Since $S_1$ is a triangle, we could use some trigonometric relations in it to solve for $S_1$, and since the area of a circular sector is known, we could solve for $S_2$ (and $S_2^{\prime\prime}$, and very innocently find that actually $S_2=S_2^{\prime\prime}$)

The main problem I have is that I don't know the inner angle of the circle sectors, because of the (seemingly randomly placed) intersection points near the borders of the rectangle.

IF ONLY I were able to locate those intersection points using pure trigonometry and geometric relationships/theorems, the problem could be solved.

Any hints or ideas?

PD: Please, don't question my (foolish) decision of not making use of symmetry. I want to take this problem as a personal challenge. Obviously, if this were to be solved quickly I wouldn't scratch my head too much and go for the easy solution.

Jose Lopez Garcia
  • 988
  • 1
    I am not sure why the symmetry argument isn't a "pure geometry" approach. You prove the congruence of the different areas given. Looks like you are looking for more of a trigonometric approach. – Doug M Jul 29 '16 at 21:36
  • 2
    Possible duplicate of, or question similar to, http://math.stackexchange.com/questions/1874736/any-smart-ideas-on-finding-the-area-of-this-shaded-region/1875264#1875264 – David Quinn Jul 29 '16 at 21:59
  • Thanks for noticing that, @DavidQuinn. When I looked for an answer I didn't find anything, or at least anything with a relevant title, that would be related with my problem. – Jose Lopez Garcia Jul 29 '16 at 22:12

5 Answers5

4

From the lower left-hand corner of the rectangle (let's call that point $A$), consider the diagonal line as a secant line of the left-hand circle, intersecting the circle at points $B$ and $C$, where $B$ is between $A$ and $C$. Also consider one of the edges of the rectangle adjacent to $A$ as a tangent line touching the circle at $D$.

Then by a theorem about tangent and secant lines from a point outside a circle, we have the following relationship of the lengths of the segments from $A$ to each of the three points $B$, $C$, and $D$: $$ (AD)^2 = AB \times AC. \tag1 $$

It is easy to find that $AD = \frac12a$. Now let $E$ be the midpoint of the bottom side of the rectangle; then $AC$ is the hypotenuse of right triangle $\triangle AEC$, which has legs $a$ and $\frac12a$, and therefore $AC = (\frac12\sqrt5)a$.

We can then use Equation $(1)$ to find the length $AB$, so we can find the length of the chord $BC$; from that chord and the radius of the circle we can get the angle of $S_1$ at the center of the circle.

David K
  • 108,155
  • Hey @DavidK, this is the kind of answer I was looking for from a beginning. Pure synthetic geometry with a theorem involved in-between. By the way, how is that theorem called? PD: The solution I get is $BC=2a/\sqrt{5}$. PD2: Once I get the sector angle, how would I go ahead and solve for $S_2$ (which would ultimately allow me to compute the shaded area)? Using a pure geometric approach, like yours. A simple hint will do. – Jose Lopez Garcia Jul 29 '16 at 22:55
  • 1
    To get the area $S_2$, you need the inverse sine of $2/\sqrt 5$. The angle of arc of $S_2$ is not a particularly nice angle, so I don't think the expression for the area is going to be as "geometric" as the way you can express the area $S_1$. I think it's going to have either $\sin^{-1}$ or a decimal approximation in it. – David K Jul 30 '16 at 00:13
  • Just the kind of answer I was looking for. Thanks again, @DavidK, for your time. – Jose Lopez Garcia Jul 30 '16 at 01:25
3

I don't know if this is what you want but.

The triangle marked $S_1$ is a isosceles triangle with base angle $= \tan^{-1} \frac 12$,
This makes the vertex angle (v) equal to $v = \pi - 2\tan^{-1} \frac 12$ Which means that $A_{sector} = S_1 + S_2 = \frac 12(\frac a2)^2 (\pi - 2\tan^{-1} \frac 12)$

$A_{S_1} = $$(\frac a2)^2 \frac 12 \sin v\\ (\frac a2)^2 \sin (2\tan^{-1} \frac 12)\\ (\frac a2)^2 2 \frac 1{\sqrt5} \frac 2{\sqrt5}\\ a^2 \frac 15$

Doug M
  • 58,694
  • I think I like this better than my own answer. It's so much more direct. – David K Jul 29 '16 at 21:56
  • Hey @DougM, I don't understand why $v=\pi-2\tan^{-1}\frac12$, more specifically the part $-2\tan^{-1}\frac12$. I can't see how this relates with the fact of the base angle being $\tan^{-1}\frac12$. – Jose Lopez Garcia Jul 29 '16 at 22:23
  • @JosePerez The base angles equal $\tan^{-1} \frac 12, 180$ degrees ($\pi $ radians) in a triangle. The vertex is $180$ less the two base angles $= \pi - 2 \tan^{-1} \frac 12$ – Doug M Aug 01 '16 at 15:25
2

Is analytic geometry all right?

Take the center of the rectangle as the origin. The two circles have the equations

$$(x \pm (a/2))^2 + y^2 = a^2/4.$$

The diagonal has the equation

$$2x=y.$$

Solving for these will give you the four points of intersection.

To get the central angles then you can use the Law of Sines after finding the length of the chords.

John
  • 26,582
  • Hey John, thanks for the attempt. But I was thinking more about Synthetic geometry (or pure geometry), which is I think the most difficult approach to take. – Jose Lopez Garcia Jul 29 '16 at 21:45
-1

I think you can consider the full rectangle area 2a^2 subtracting the areas of two circles then devide the result by 2.

AMMAR AL-SHAIKHLI
  • 1
  • This is not a full answer, and is more suitable for a comment. And consider using MathJax to improve your formatting. – Cave Johnson Sep 21 '16 at 03:53
-1

Jose Perez You can find the angle between diagonal and length by using x=inv.tan (2R/4R)

It is equal to the angle of triangle s1 (alternating angles). And there you go, angle of sector s 180-2x.

Deechit Poudel
  • 1
  • The idea of using $\arctan (1/2)$ has been mentioned in previous Answers. From the quick remark you posted it is hard to know what justification is offered; "alternating angles" seems to be about symmetry that the OP wants to avoid. Since a good bit of time passed since the Question was posted, a hasty reply is not of much benefit. – hardmath Nov 24 '16 at 15:34