Evaluate the integral $ \int_{-\infty}^{\infty} {\sin ^2 (x) \over x^2 (x^2 + 1)}\:dx$

Question

Can we evaluate the integral using Jordan lemma? $$ \int_{-\infty}^{\infty} {\sin ^2 (x) \over x^2 (x^2 + 1)}\:dx$$

What de we do if removeable singularity occurs at the path of integration?

Answer 1

Using $\sin^2(z)=\frac12(1-\cos(2z))$, you should be able to handle this in much the same way as this answer.

---

Details (modified from the answer mentioned above)

Since $\lim\limits_{z\to0}\frac{1-\cos(2z)}{2z^2}=1$, the singularity of the integrand near $z=0$ is removable. Therefore, since the integrand vanishes for $z$ within $\frac12$ of the real axis as $|z|\to\infty$ and there are no singularities within $\frac12$ of the real axis, the integral does not change when shifting the path of integration from $z=t$ to $z=t-\frac{i}{2}$.

Now we can break up the integral as $$ \int_{-\infty-i/2}^{\infty-i/2}\frac{1-\cos(2z)}{2z^2(z^2+1)}\,\mathrm{d}z =\frac14\int_{\gamma^+}\frac{1-e^{2iz}}{z^2(z^2+1)}\mathrm{d}z +\frac14\int_{\gamma^-}\frac{1-e^{-2iz}}{z^2(z^2+1)}\mathrm{d}z\tag{1} $$ where $\gamma^+$ and $\gamma^-$ are as depicted below:

$\hspace{4.6cm}$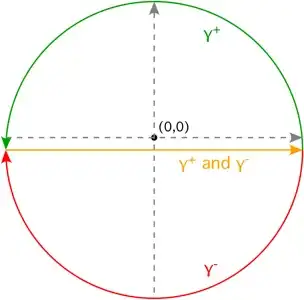

$\gamma^+$ circles two singularities ($z=0$ and $z=i$) clockwise, and $\gamma^-$ circles one singularity ($z=-i$) counter-clockwise.

All of the singularities are simple, so to get the residue at $z=z_0$, we just need to multiply by $z-z_0$ and taking $\displaystyle\lim_{z\to z_0}$

At $z=0$ the residue of $\displaystyle\frac{1-e^{2iz}}{z^2(z^2+1)}$ is $-2i$

At $z=i$ the residue of $\displaystyle\frac{1-e^{2iz}}{z^2(z^2+1)}$ is $\displaystyle\frac{1-e^{-2}}{-2i}$

At $z=-i$ the residue of $\displaystyle\frac{1-e^{-2iz}}{z^2(z^2+1)}$ is $\displaystyle\frac{1-e^{-2}}{2i}$

Putting these together with $(1)$ yields $$ \begin{align} \int_{-\infty}^\infty\frac{1-\cos(z)}{z^2(z^2+1)}\,\mathrm{d}z &=\frac{2\pi i}{4}\left(-2i+\frac{1-e^{-2}}{-2i}\right)-\frac{2\pi i}{4}\left(\frac{1-e^{-2}}{2i}\right)\\ &=\frac{\pi}{2}\left(2-\frac{1-e^{-2}}{2}-\frac{1-e^{-2}}{2}\right)\\ &=\frac\pi2+\frac{\pi}{2e^2}\tag{2} \end{align} $$

Answer 2

Taking $$C_R:=[-R,-\epsilon]\cup\left(\gamma_\epsilon:=\{z=\epsilon e^{it}\;\;|\;\;0\leq t\leq \pi\}\right)\cup [\epsilon,R]\cup\left(\gamma_R:=\{z=Re^{it}\;\;|\;\;0\leq t\leq \pi\}\right)$$ $$f(z)=\frac{1-e^{2iz}}{z^2(z^2+1)}$$
we get $$\oint_{C_R}\frac{1-e^{2iz}\,dz}{z^2(z^2+1)}=2\pi i\,Res_{z=i}(f)=2\pi i\frac{1-e^{-2}}{i^2(2i)}=-\pi\left(1-e^{-2}\right)$$ But $$\oint_{C_R}f\,dz=\int_{-R}^{-\epsilon} f\,dx\,-\int_{\gamma_\epsilon}f\,dz+\int_\epsilon^Rf\,dx+\int_{\gamma_R}f\,dz$$ Using now the nice lemma in the answer here , we get $$\lim_{\epsilon\to 0}\int_{\gamma_\epsilon}f(z)dz=-i\pi\,Res_{z=0}(f)=-i\pi(-2i)=-2\pi$$ And either using Jordan's lemma or directly: $$\left|\int_{\gamma_R}f(z)\,dz\right|\leq \frac{1+e^{-2R\sin t}}{R^2(R^2-1)}\pi R\xrightarrow [R\to\infty]{}0$$ So passing to the limit when $\epsilon\to 0\,\,,\,\,R\to\infty\,$ and using Cauchy's Integral Theorem, we get: $$\int_{-\infty}^\infty \frac{2\sin^2x\,dx}{x^2(x^2+1)}=2\pi-\pi(1-e^{-2})=\pi\left(1+\frac{1}{e^2}\right)\Longrightarrow $$ $$\Longrightarrow\int_{-\infty}^\infty\frac{\sin^2 x\,dx}{x^2(x^2+1)}=\frac{\pi}{2}\left(1+\frac{1}{e^2}\right)$$

Answer 3

Hint, note that $ \cos(2x)=1-2\sin(x)^2 $, this suggest to consider the integral

$$ \int_{C} \frac{ {\rm e}^{2 i z} - 1 }{ z^2 (z^2 + 1)} dz \,.$$

Answer 4

Noticing that $$ \int_{-\infty}^{\infty} {\sin ^2 (x) \over x^2 (x^2 + 1)}\:dx= \frac{1}{2} \int_{-\infty}^{\infty} \frac{1-\cos (2 x)}{x^2\left(x^2+1\right)} $$

Let’s consider the parameterised integral

$\displaystyle I(a)=\int_{-\infty}^{\infty} \frac{1-\cos (a x)}{x^2\left(x^2+1\right)} d x \textrm{ for }a>0 \tag*{} $

and then differentiate $I(a)$ once and twice w.r.t. $a$ and obtain $\displaystyle \begin{aligned} & I^{\prime}(a)=\int_{-\infty}^{\infty} \frac{\sin (a x)}{x\left(x^2+1\right)} d x \\ & I^{\prime \prime}(a)=\int_{-\infty}^{\infty} \frac{\cos (a x)}{x^2+1} d x=\pi e^{-a}\end{aligned}\tag*{} $ Integrating back yields

$\displaystyle I^{\prime}(a)=-\pi e^{-a}+C_1 \Rightarrow C_1=I^{\prime}(0)+\pi=\pi\tag*{} $

Integrating back again yields $\displaystyle I(a)=\pi e^{-a}+\pi a+C_2 \Rightarrow C_2=-\pi\tag*{} $

We can conclude that $\displaystyle \int_{-\infty}^{\infty} \frac{1-\cos (a x)}{x^2\left(x^2+1\right)} d x=\pi\left(e^{-a}+a-1\right)\tag*{} $

In particular, when $a=2$, we have $\boxed{\displaystyle \int_{-\infty}^{\infty} \frac{\sin ^2 x}{x^2\left(x^2+1\right)} d x=\frac{\pi}{2}\left(1+\frac{1}{e^2}\right) }\tag*{} $