Ways to go from A to B(proof)

Question

We know that the ways to go from A to B in a $m×n$ rectangle is $(m+n)!/m!n!$ I want a proof for this formula.(the way should be the shortest.

My Attempt:There is a counting way that may help us.

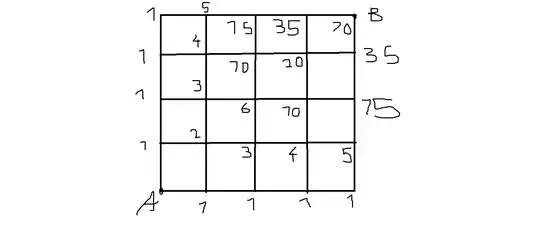
Every point is calculated by the sum of two adjacent points.

Presumably you require that each step either takes you up or to the right? If so then there are $m$ left steps to take and $n$ up steps...the order doesn't matter so it's just a question of where you put the up steps amongst the $n=m$ total so.... — lulu, Jun 01 '16 at 10:39

score 3 · Accepted Answer · answered Jun 01 '16 at 10:59

3

When considering the possible paths,we say "Up, right, up, right...". Using "u" and "r" . We can write out a path $$\underbrace{r,r,r,\ldots ,r}_{m}\,\,\underbrace{u,u,u,\ldots ,u}_{n}$$ so there are $\frac{(m+n)!}{m!n!}$ codes or paths..

answered Jun 01 '16 at 10:59

Behrouz Maleki

11,342

score 0 · Answer 2 · edited Apr 13 '17 at 12:21

0

See

Lattice paths and Catalan Numbers

or

How can I find the number of the shortest paths between two points on a 2D lattice grid?

or

Lattice Paths Question

or google for "Counting Paths on a Grid" to find other links, even some videos.

edited Apr 13 '17 at 12:21

Community

1

answered Jun 01 '16 at 10:47

user340508

921

Ways to go from A to B(proof)

2 Answers2

Linked