2

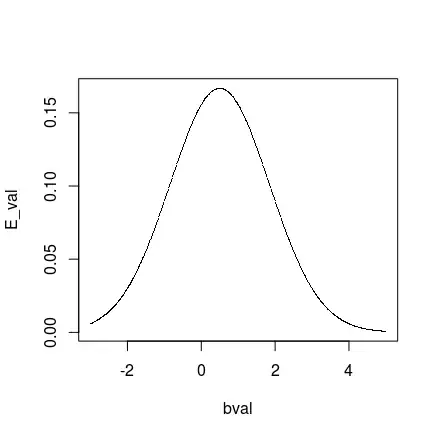
Suppose I want the expectation, $E\Phi(X-\mu)\Phi(\mu-X)$, where $\Phi(.)$ represents the Normal CDF, and X is $Normal(\beta,1)$. Consequently $\Phi(.)$'s are uniform[0,1] and at the same time two uniforms are negatively correlated (antithetic variables).

Let, $E\Phi(X-\mu)\Phi(\mu-X)=EU(1-U)=EUV$, which is basically a product of two uniforms. Now if I use the cdfs as uniformly distributed and find the expectation based on uniform distribution, i.e., finding distribution of UV and use that to compute $EUV$, I loose information about $\beta$. Does anyone have any idea how to get the expectation without loosing any information about $\beta$?

Thank you

Shakil
  • 101

1 Answers1

2

$\Phi(.)$'s are not uniform on $[0,1]$ if $\mu \neq \beta$.

This idea comes from the fact that: $Y=F(X) \sim Unif[0,1]$ if $F$ is a CDF of $X$. In your case, $\Phi(X-\mu)$ is CDF of $Z \sim N(\beta-\mu,1)$. So at least the drift $\mu$ matters in this expectation, that can be interpreted as expectation $E[g(x)]$ of the function $g(x) = \Phi(\mu-x)\Phi(x-\mu)$ for $X \sim N(\beta, 1)$.

$$E = \int [\Phi(\mu-x)\Phi(x-\mu)] \cdot f_{\beta,1}(x)dx $$

I've made a simulation in $R$ where I have fixed $\mu=0.5$ and ranged $\beta$ from $-3$ to $4$. If everything is correct, that shows that values of expectation somehow follow normal distribution with the mean supposed to be $0.5$:

plot1

mu<-0.5

f <- function(x,b){
  # Function under integral for expectation: X has density with 
  # parameters mean = b, sd = 1;
  # both normal CDFs have default parameters (0;1)
  pnorm(mu - x)*(1-pnorm(mu - x))*dnorm(x,mean=b,sd=1)

}

# Actual expectation
E_val_f= function(b) {integrate(f,lower=-Inf,upper=Inf,b=b)$value}

bval<-seq(from=-3,to=5, by=0.01) # Beta values
E_val<-sapply(bval,E_val_f) # expectation values

# Picture
plot(bval,E_val,pch=".")
Community
  • 1
Slowpoke
  • 862