Modelling the "Moving Sofa"

Question

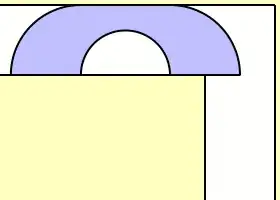
I believe that many of you know about the moving sofa problem; if not you can find the description of the problem here.

In this question I am going to rotate the L shaped hall instead of moving a sofa around the corner. By rotating the hall $180^{\circ}$ what remains between the walls will give the shape of the sofa. Like this:

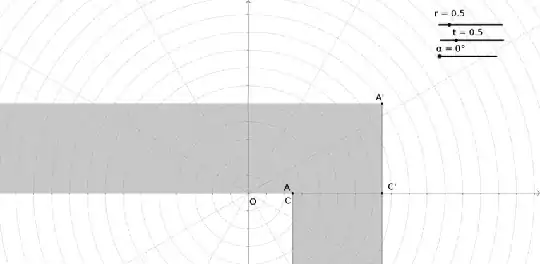
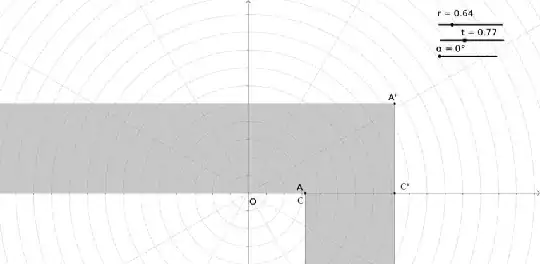
The points on the hall have the following properties:

\begin{eqnarray} A & = & \left( r\cos { \alpha } ,t\sin { \alpha } \right) \\ { A }' & = & \left( r\cos { \alpha } +\sqrt { 2 } \cos { \left( \frac { \pi }{ 4 } +\frac { \alpha }{ 2 } \right) } ,t\sin { \alpha } +\sqrt { 2 } \sin { \left( \frac { \pi }{ 4 } +\frac { \alpha }{ 2 } \right) } \right) \\ { B } & = & \left( r\cos { \alpha } -\frac { t\sin { \alpha } }{ \tan { \left( \frac { \alpha }{ 2 } \right) } } ,0 \right) \\ { B }' & = & \left( r\cos { \alpha } -\frac { t\sin { \alpha } }{ \tan { \left( \frac { \alpha }{ 2 } \right) } } -\frac { 1 }{ \sin { \left( \frac { \alpha }{ 2 } \right) } } ,0 \right) \\ C & = & \left( r\cos { \alpha } +t\sin { \alpha } \tan { \left( \frac { \alpha }{ 2 } \right) } ,0 \right) \\ { C }' & = & \left( r\cos { \alpha } +t\sin { \alpha } \tan { \left( \frac { \alpha }{ 2 } \right) } +\frac { 1 }{ \cos { \left( \frac { \alpha }{ 2 } \right) } } ,0 \right) \end{eqnarray}

Attention: $\alpha$ is not the angle of $AOC$, it is some angle $ADC$ where $D$ changes location on $x$ axis for $r\neq t$. I am saying this because images can create confusion. Anyways I will change them as soon as possible.

I could consider $r=f(\alpha)$ and $t=g(\alpha)$ but for this question I am going to take $r$ and $t$ as constants. If they were functions of $\alpha$ there would appear some interesting shapes. I experimented for different functions however the areas are more difficult to calculate, that's why I am not going to share. Maybe in the future.

We rotate the hall for $r=t$ in the example above:
In this case:

1. point A moves on a semicircle
2. The envelope of lines between A' and C' is a circular arc. One has to prove this but I assume that it is true for $r=t$.

If my second assumption is correct the area of sofa is $A= 2r-\frac { \pi r^{ 2 } }{ 2 } +\frac { \pi }{ 2 } $. The maximum area is reached when $r = 2/\pi$ and it's value is: $$A = 2/\pi+\pi/2 = 2,207416099$$

which matches with Hammersley's sofa. The shape is also similar or same:

Now I am going to increase $t$ with respect to $r$. For $r=2/\pi$ and $t=0.77$:

Well, this looks like Gerver's sofa.

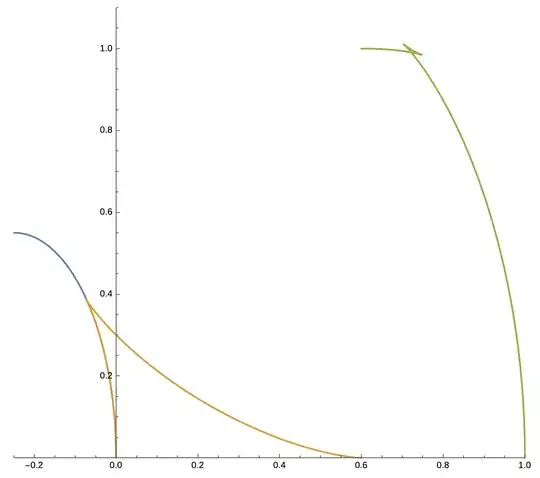
I believe thearea can be maximized by finding the equations of envelopes above and below the sofa. Look at this question where @Aretino has computed the area below $ABC$.

I don't know enough to find equations for envelopes. I am afraid that I will make mistakes. I considered to calculate area by counting number of pixels in it, but this is not a good idea because for optimizing the area I have to create many images.

I will give a bounty of 200 for whom calculates the maximum area. As I said the most difficult part of the problem is to find equations of envelopes. @Aretino did it.

PLUS: Could following be the longest sofa where $(r,t)=((\sqrt 5+1)/2,1)$ ?

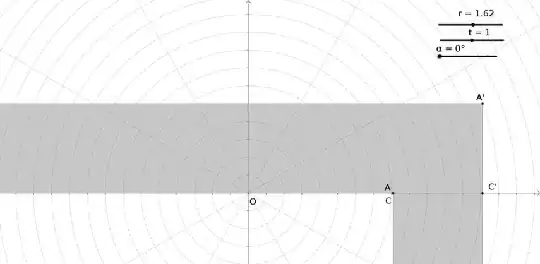
If you want to investigate further or use animation for educational purposes here is the Geogebra file: http://ggbm.at/vemEtGyj

---

Ok, I had some free time and I count number of pixels in the sofa and I am sure that I have something bigger than Hammersley's constant.

First, I made a simulation for Hammersley's sofa where $r=t=2/\pi$ and exported the image to png in 300 dpi (6484x3342 pixels) and using Gimp counted number of pixels which have exactly same value. For Hammersley I got $3039086$ pixels.

For the second case $r=0.59$ and $t=0.66$ and I got $3052780$ pixels. To calculate area for this case:

$$\frac{3052780}{3039086}(2/\pi + \pi/2)=2.217362628$$

which is slightly less than Gerver's constant which is $2.2195$. Here is the sofa:

Answer 1

WARNING: this answer uses the new parameterization of points introduced by the OP: \begin{eqnarray} A & = & \left( r\cos { \alpha } ,t\sin { \alpha } \right) \\ { A }' & = & \left( r\cos { \alpha } +\sqrt { 2 } \cos { \left( \frac { \pi }{ 4 } +\frac { \alpha }{ 2 } \right) } ,t\sin { \alpha } +\sqrt { 2 } \sin { \left( \frac { \pi }{ 4 } +\frac { \alpha }{ 2 } \right) } \right) \\ C & = & \left( r\cos { \alpha } +t\sin { \alpha } \tan { \left( \frac { \alpha }{ 2 } \right) } ,0 \right) \\ { C }' & = & \left( r\cos { \alpha } +t\sin { \alpha } \tan { \left( \frac { \alpha }{ 2 } \right) } +\frac { 1 }{ \cos { \left( \frac { \alpha }{ 2 } \right) } } ,0 \right) \end{eqnarray}

Another parameterization, which also apperaed in a first version of this question, was used in a previous answer to a related question.

The inner shape of the sofa is formed by the ellipse of semiaxes $r$, $t$ and by the envelope of lines $AC$ (here and in the following I'll consider only that part of the sofa in the $x\ge0$ half-plane).

The equations of lines $AC$ can be expressed as a function of $\alpha$ ($0\le\alpha\le\pi$) as $F(x,y,\alpha)=0$, where: $$ F(x,y,\alpha)= -t y \sin\alpha \tan{\alpha\over2} - t \sin\alpha \left(x - r \cos\alpha - t \sin\alpha \tan{\alpha\over2}\right). $$ The equation of the envelope can be found from: $$ F(x,y,\alpha)={\partial\over\partial\alpha}F(x,y,\alpha)=0, $$ giving the parametric equations for the envelope: $$ \begin{align} x_{inner}=& (r-t) \cos\alpha+\frac{1}{2}(t-r) \cos2\alpha+\frac{1}{2}(r+t),\\ y_{inner}=& 4 (t-r) \sin\frac{\alpha}{2}\, \cos^3\frac{\alpha}{2}.\\ \end{align} $$

We need not consider this envelope if $t<r$, because in that case $y_{inner}<0$. If $t>r$ the envelope meets the ellipse at a point $P$: the corresponding value of $\alpha$ can be found from the equation $(x_{inner}/r)^2+(y_{inner}/t)^2=1$, whose solution $\alpha=\bar\alpha$ is given by: $$ \begin{cases} \displaystyle\bar\alpha= 2\arccos\sqrt{t\over{t+r}}, &\text{for $t\le3r$;}\\ \displaystyle\bar\alpha= \arccos\sqrt{t\over{2(t-r)}}, &\text{for $t\ge3r$.}\\ \end{cases} $$

The corresponding values $\bar\theta$ for the parameter of the ellipse can be easily computed from: $\bar\theta=\arcsin(y_{inner}(\bar\alpha)/t)$: $$ \begin{cases} \displaystyle\bar\theta= \arcsin\frac{4 \sqrt{rt} (t-r)}{(r+t)^2}, &\text{for $t\le3r$;}\\ \displaystyle\bar\theta= \arcsin\frac{\sqrt{t(t-2 r)}}{t-r}, &\text{for $t\ge3r$.}\\ \end{cases} $$

For $t\ge r$ we can then represent half the area under the inner shape of the sofa as an integral: $$ {1\over2}Area_{inner}=\int_0^{2t-r} y\,dx= \int_{\pi/2}^{\bar\theta}t\sin\theta{d\over d\theta}(r\cos\theta)\,d\theta+ \int_{\bar\alpha}^{\pi} y_{inner}{dx_{inner}\over d\alpha}\,d\alpha. $$

This can be computed explicitly, here's for instance the result for $r<t<3r$: $$ \begin{align} {1\over2}Area_{inner}= {\pi\over4}(r^2-rt+t^2) +\frac{1}{48} (t-r)^2 \left[-24 \cos ^{-1}\frac{\sqrt{t}}{\sqrt{r+t}} +12 \sin \left(2 \cos^{-1}\frac{\sqrt{t}}{\sqrt{r+t}}\right)\\ +12 \sin \left(4 \cos^{-1}\frac{\sqrt{t}}{\sqrt{r+t}}\right) -4 \sin \left(6 \cos^{-1}\frac{\sqrt{t}}{\sqrt{r+t}}\right) -3 \sin \left(8 \cos^{-1}\frac{\sqrt{t}}{\sqrt{r+t}}\right) \right]\\ -2 r t {\sqrt{rt} |r^2-6 r t+t^2|\over(r+t)^4} -{1\over4} r t \sin ^{-1}\frac{4 \sqrt{rt} (t-r)}{(r+t)^2}\\ \end{align} $$

The outer shape of the sofa is formed by line $y=1$ and by the envelope of lines $A'C'$. By repeating the same steps as above one can find the parametric equations of the outer envelope: $$ \begin{align} x_{outer}&= (r-t) \left(\cos\alpha-{1\over2}\cos2\alpha\right) +\cos\frac{\alpha}{2}+{1\over2}(r+t)\\ y_{outer}&= \sin\frac{\alpha}{2} \left(-3 (r-t) \cos\frac{\alpha}{2} +(t-r) \cos\frac{3 \alpha}{2}+1\right)\\ \end{align} $$ This curve meets line $y=1$ for $\alpha=\pi$ if $t-r\le\bar x$, where $\bar x=\frac{1}{432} \left(17 \sqrt{26 \left(11-\sqrt{13}\right)}-29 \sqrt{2 \left(11-\sqrt{13}\right)}\right)\approx 0.287482$. In that case the intersection point has coordinates $(2t-r,1)$ and the area under the outer shape of the sofa can be readily found: $$ {1\over2}Area_{outer}={1\over3}(r+2t)+{\pi\over4}(1-(t-r)^2) $$ If, on the other hand, $t-r>\bar x$ then one must find the value of parameter $\alpha$ at which the envelope meets the line, by solving the equation $y_{outer}=1$ and looking for the smallest positive solution. This has to be done, in general, by some numerical method.

The area of the sofa can then be found as $Area_{tot}=Area_{outer}-Area_{inner}$. I used Mathematica to draw a contour plot of this area, as a function of $r$ (horizontal axis) and $t$ (vertical axis):

There is a clear maximum in the region around $r = 0.6$ and $t = 0.7$. In this region one can use the simple expressions for $Area_{inner}$ and $Area_{outer}$ given above, to find the exact value of the maximum. A numerical search gives $2.217856997942074266$ for the maximum area, reached for $r=0.605513519698965$ and $t=0.6678342468712839$.

Answer 2

This is not an answer to the stated question, just an outline and an example of how to compute the envelope (and thus area) numerically, pretty efficiently.

The code seems to work, but it is not tested, or nowhere near optimal in the algorithmic level; it is just a rough initial sketch to explore the problem at hand.

The sofa is symmetric with respect to the $x$ axis, so we only need to consider the (positive $x$) half plane. If we use $\alpha$ for the rotation, $\alpha \in [0, \pi]$, the initially vertical walls (on the right side) are the only ones we need to consider. For simplicity, I'll use $r_x$ and $r_y$ for the radiuses (OP used $r$ and $t$, respectively).

The equation for the points that form the near side wall ($t \ge 0$) is $$\vec{p}_{nw}(t, \alpha) = \begin{cases} x_{nw}(t, \alpha) = r_x \cos(\alpha) + t \sin(\alpha/2)\\ y_{nw}(t, \alpha) = r_y \sin(\alpha) - t \cos(\alpha/2)\end{cases}$$

Setting $x_{nw}(t, \alpha) = x$, solving for $t$, and substituting into $y_{nw}(t, \alpha)$ yields $$y_n(x, \alpha) = r_y \sin(\alpha) + \frac{r_x \cos(\alpha) - x}{\tan(\alpha/2)}$$ Because the near wall starts at angle $\alpha$, we must only consider $x \ge x_n(0,\alpha)$. We can do that in practice by defining $$\alpha_0(x) = \left\lbrace\begin{matrix} r_y\sqrt{1 - \left(\frac{x}{r_x}\right)^2},&x \lt r_x\\ 0,&x \ge r_x\end{matrix}\right.$$ and only considering $\alpha_0 \le \alpha \le \pi$ when evaluating $y_n(x,\alpha)$. It reaches its maximum when its derivative, $$\frac{d y_n(x,\alpha)}{d \alpha} = \frac{x - r_x}{1 - \cos(\alpha)} - (r_x - r_y)\cos(\alpha)$$ is zero. There may be two real roots, $$\begin{align}\alpha_1(x) &= \arccos\left(\frac{\sqrt{ (r_x - r_y)(5 r_x - r_y - 4 x)} + (r_x - r_y)}{2 ( r_x - r_y )}\right)\\ \alpha_2(x) &= \pi - \arccos\left(\frac{\sqrt{ (r_x - r_y)(5 r_x - r_y - 4 x)} - (r_x - r_y)}{2 ( r_x - r_y )}\right)\end{align}$$ In summary, the near wall is the maximum of one, two, or three values: $y_n(x,\alpha_0)$; $y_n(x,\alpha_1)$ if $\alpha_0 \lt \alpha_1 \lt \pi$; and $y_n(x,\alpha_2$) if $\alpha_0 \lt \alpha_2 \lt \pi$.

For the far side wall, the points are $$\vec{p}_f(t, \alpha) = \begin{cases} x_f(t) = r_x \cos(\alpha) + \cos(\alpha/2) + \sin(\alpha/2) + t \sin(\alpha/2)\\ y_f(t) = r_y \sin(\alpha) + \sin(\alpha/2) - \cos(\alpha/2) - t \cos(\alpha/2)\end{cases}$$ The first added term represents the corridor width, and the second the corridor height, both $1$. Setting $x_f(t, \alpha) = x$, solving for $t$, and substituting into $y_f(t, \alpha)$ yields $$y_f(x, \alpha) = \frac{(r_x + r_y - 2x)\cos(\alpha/2) + (r_x - r_y)\cos(3\alpha/2) + 2 }{2 \sin(\alpha/2)}$$ Its derivative is $$\frac{d y_f(x, \alpha)}{d \alpha} = \frac{rx - x + \cos(\alpha/2)}{\cos(\alpha) - 1} - \cos(\alpha)(r_x - r_y)$$ It can have up to four real roots (the roots of $4(r_x-r_y)\chi^4 - 6(r_x-r_y)\chi^2 - \chi + (r_x - r_y) + (x - r_y) = 0$). While it does have analytical solutions, they are nasty, so I prefer to use a binary search instead. I utilize the fact that the sign (and zeros) of the derivative are the same as the simpler function $$d_f(x, \alpha) = \cos(\alpha)\left(\cos(\alpha)-1\right)(r_x - r_y) - \cos(\alpha/2) - r_x + x$$ which does not have poles at $\alpha=0$ or $\alpha=\pi$.

Here is an example implementation in C:

#include <stdlib.h>
#include <string.h>
#include <stdio.h>
#include <math.h>

#define PI 3.14159265358979323846

static double near_y(const double x,
                     const double xradius,
                     const double yradius)
{
    double y = (x < xradius) ? yradius * sqrt(1.0 - (x/xradius)*(x/xradius)) : 0.0;
    if (xradius != yradius) {
        const double a0 = (x < xradius) ? acos(x/xradius) : 0.0;
        const double s  = (xradius - yradius)*(5*xradius - yradius - 4*x);
        if (s >= 0.0) {
            const double r = 0.5 * sqrt(s) / (xradius - yradius);
            if (r > -1.5 && r < 0.5) {
                const double a1 = acos(r + 0.5);
                if (a1 > a0 && a1 < PI) {
                    const double y1 = yradius * sin(a1) + (xradius * cos(a1) - x) / tan(0.5 * a1);
                    if (y < y1)
                        y = y1;
                } 
            }
            if (r > -0.5 && r < 1.5) {
                const double a2 = PI - acos(r - 0.5);
                if (a2 > a0 && a2 < PI) {
                    const double y2 = yradius * sin(a2) + (xradius * cos(a2) - x) / tan(0.5 * a2);
                    if (y < y2)
                        y = y2;
                }
            }
        }
    }
    return y;
}

Above, near_y() finds the maximum $y$ coordinate the near wall reaches at point $x$.

static double far_y(const double x,
                    const double xradius,
                    const double yradius)
{
    const double rxy = xradius - yradius;
    const double rx = xradius - x;
    double       retval = 1.0;
    double       anext = 0.0;
    double       dnext = x - 1.0 - xradius;
    double       acurr, dcurr, y;

    /* Outer curve starts at min(1+xradius, 2*yradius-xradius). */
    if (x < 1.0 + xradius && x < yradius + yradius - xradius)
        return 1.0;

    while (1) {
        acurr = anext;
        dcurr = dnext;
        anext += PI/1024.0;
        if (anext >= PI)
            break;
        dnext = cos(anext)*(cos(anext) - 1.0)*rxy - cos(anext*0.5) - rx;

        if ((dcurr < 0.0 && dnext > 0.0) ||
            (dcurr > 0.0 && dnext < 0.0)) {
            double amin = (dcurr < 0.0) ? acurr : anext;
            double amax = (dcurr < 0.0) ? anext : acurr;
            double a, d;
            do {
                a = 0.5 * (amin + amax);
                d = cos(a)*(cos(a)-1.0)*rxy - cos(a*0.5) - rx;
                if (d < 0.0)
                    amin = a;
                else
                if (d > 0.0)
                    amax = a;
                else
                    break;
            } while (amax > amin && a != amin && a != amax);
            y = (cos(0.5*a)*(0.5*(xradius+yradius)-x) + cos(1.5*a)*rxy*0.5 + 1.0) / sin(0.5*a);
            if (retval > y) {
                retval = y;
                if (y <= 0.0)
                    return 0.0;
            }
        } else
        if (dcurr == 0.0) {
            y = (cos(0.5*acurr)*(0.5*(xradius+yradius)-x) + cos(1.5*acurr)*rxy*0.5 + 1.0) / sin(0.5*acurr);
            if (retval > y) {
                y = retval;
                if (y <= 0.0)
                    return 0.0;
            }
        }
    }
    return retval;
}

Above, far_y() finds the minimum $y$ coordinate for the far wall at $x$. the far wall reaches at the same point. It calculates the sign of the derivative for 1024 values of $\alpha$, and uses a binary search to find the root (and the extremum $y$) whenever the derivative spans zero.

With the above two functions, we only need to divide the full sofa width ($1 + r_x$) to slices, evaluate the $y$ coordinates for each slice, multiply the $y$ coordinate difference by the double slice width (since we only calculate one half of the sofa), to obtain an estimate for the sofa area (using the midpoint rule for the integral):

double sofa_area(const unsigned int xsamples,
                 const double       xradius,
                 const double       yradius)
{
    if (xradius > 0.0 && yradius > 0.0) {
        const double dx = (1.0 + xradius) / xsamples;
        double       area = 0.0;
        unsigned int i;
        for (i = 0; i < xsamples; i++) {
            const double x = dx * (0.5 + i);
            const double ymin = near_y(x, xradius, yradius);
            const double ymax = far_y(x, xradius, yradius);
            if (ymin < ymax)
                area += ymax - ymin;
        }        
        return 2*dx*area;
    } else
        return 0.0;
}

As far as I have found, the best one is sofa_area(N, 0.6055, 0.6678) = 2.21785 (with N ≥ 5000, larger N yields more precise estimates; I checked up to N = 1,000,000).

The curve the inner corner makes ($(x_{wn}(0,\alpha), y_{wn}(0,\alpha))$, $0 \le \alpha \le \pi$) is baked inside near_y() and far_y() functions. However, it would be possible to replace $y_{wn}(0,\alpha)$ with a more complicated function (perhaps a polynomial scaling $r_y$, so that it is $1$ at $\alpha = 0, \pi$?), if one re-evaluates the functions above. I personally use Maple or Mathematica for the math, so the hard part, really, is to think of a suitable function that would allow "deforming" the elliptic path in interesting ways, without making the above equations too hard or slow to implement.

The C code itself could be optimized, also. (I don't mean micro-optimizations; I mean things like using the trapezoid rule for the integral, better root finding approach for far_y(), and so on.)

Answer 3

The envelope of $A'C'$ is not monotonic in some cases, which was not considered in the above analytical answers.

$a=0.25, b=0.55$

Blue: trajactory of $A$ Orange: envelope of $AC$ Green: envelope of $A'C'$