Example of Pairwise Independent but not Jointly Independent Random Variables?

Question

I am asked to:

Find a joint probability distribution $P(X_1,\dots, X_n)$ such that $X_i , \, X_j$ are independent for all $i \neq j$, but $(X_1, \dots , X_n)$ are not jointly independent.

I have no idea where to start, please help.

Answer 1

I always remember this clear example from Probability Essentials, chapter 3, by J.Jacod & P.Protter.

Let $\Omega = \{1,2,3,4\}$, and $\mathscr{A} = 2^\Omega$. Let $P(i) = \frac{1}{4}$, where $i = 1,2,3,4$.

Let $A = \{1,2\}$, $B = \{1,3\}$, $C = \{2,3\}$. Then A,B,C are pairwise independent but are not independent.

Answer 2

See this link: http://faculty.washington.edu/fm1/394/Materials/2-3indep.pdf

Throw two fair dice.

Consider the events:

• $A:=\{\text{the sum of the points is 7}\}$,
• $B:=\{\text{the first die rolled a 3}\}$,
• $C:=\{\text{the second die rolled a 4}\}$.

All three events have probability $\displaystyle\frac{1}{6}$.

Moreover, you can check that they are pairwise independent.

However, they are not jointly independent.

For your random variables, just take $1_A, 1_B,$ and $1_C$, the indicator functions of these events.

Answer 3

There's actually an even simpler example: Let X, Y, and Z be random variables, with X and Y independent Bernoulli(1/2) trials and Z equal to X xor Y. It's easy to verify that Z is pairwise independent with X: Once X has been decided, as long as Y remains unknown, Z has a 50% chance of being 1 or 0, regardless of what X is. Since X and Y are defined in the same way, Z must also be independent of Y. However, clearly they are not jointly independent, since Z can explicitly be determined by knowing X and Y.

One neat thing about this example is that, in addition to all variables being pairwise independent, the associativity of XOR means that they're also interchangeable. One could easily imagine extending this to more variables, with more complex distributions — say, a set of five of Binomial(n,1/2) distributions where the parity of the number of ith Bernoulli trials which are successes must be equal to the parity of i, based on the natural extension of the XOR relation — but I'll do the annoying thing all textbooks do and leave the proof of this as an exercise for the reader.

Answer 4

The definition of mutual/joint independent can be described like this:

events $A_1$, $A_2$,$...$ , $A_k$ are jointly independent if $P(A_{i_1} ∩ A_{i_2} ∩···∩ A_{i_j}) = P(A_{i_1} )P(A_{i_2})··· P(A_{i_j})$ for every subset $\{i_1,i_2,... ,i_j\}$ of $\{1, 2,... , k\}$.

In 1946 S. N. Bernstein proposed two examples and in 2007 C. Stepniak proved that they are two (and the only two) simplest examples for your request.

The two examples were illustrated as bellow:

Where each black dot represents an outcome from the sample space $S = \{110, 101, 011, 000\}$, and there are three events in each example.

For the first example, we define an event $A_k$ as taking a sample randomly from the space $S$ with 1 in the kth position. We can calculate the probability of $A_k$: $P(A_k)=\frac{1}{2}$, and we can also calculate the joint probability of any two event pairs(meaning that any two different positions are 1 at the same time, three possibilities: $110$, $101$ and $011$): $P(A_i ∩ A_j) = P(A_i)P(A_j) = \frac{1}{4}$ for $i\neq j$, but $P(A_1 ∩ A_2 ∩ A_3) = 0 \neq P(A_1)P(A_2)P(A_3)$ because $A_1 ∩ A_2 ∩ A_3 = \emptyset$, meaning that $111$ doesn't exist in the sample space $S$.

In the second example, everything remains the same but we define an event $B_k$ as taking a sample randomly from the space $S$ with 0 in the kth position. By the same token, we can calculate $P(A_i ∩ A_j)$ for every $i\neq j$: $P(A_i ∩ A_j) = P(A_i)P(A_j) = \frac{1}{4}$, but when it comes to the joint probability $P(A_1 ∩ A_2 ∩ A_3)$ we find that it becomes $\frac{1}{4}$ because $000$ is one of the four possibilities in $S$: $P(A_1 ∩ A_2 ∩ A_3) = \frac{1}{4} \neq \frac{1}{2} * \frac{1}{2} * \frac{1}{2}$. This example is equivalent to this one: Pairwise independence versus mutual independence in nature.

Thus, we can see from the two simplest examples that the bellow iff doesn't hold:

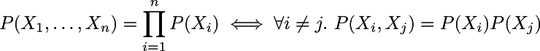
References:
1. Mutually (Jointly) Independent Events
2. Bernstein’s Examples on Independent Events

Answer 5

Hint: Let $n\ge 3$. Toss a fair coin $n-1$ times. For $i=1$ to $n-1$, let $X_i=1$ if the $i$-th toss gave a head, and $X_i=0$ otherwise. Let $X_n=1$ if the sum $\sum_1^{n-1} X_i$ is odd, and $X_n=0$ otherwise.

It is obvious that if $i\ne j$, and they are both less than $n$, then $X_i$ and $X_j$ are independent. It takes a bit more work to show that if $i\le n-1$, then $X_i$ and $X_n$ are independent. And it is clear that $X_1,\dots,X_n$ are not mutually independent, since if we know the values of the $X_1$ from $1$ to $n-1$, then we know the value of $X_n$.

Answer 6

Let $X,Y,Z$ be iid Rademacher. Then $XY,YZ,ZX$ are pariwise independent, but not jointly independent.

You can check the pairwise independence using elemetary verification of cases, or any other method you like (e.g. characteristic functions). To see the non-independence, note that $XY\cdot YZ\cdot ZX =1 $ almost surely.