Right triangle on an ellipse, find the area

Question

Beginning note: Please wait until the animations load. The loading might take some time depending on your internet connection. Secondly, the title and the content of the question might not be well understood. Any edit is welcome.

Suppose that I have a right triangle $\triangle ABC$ where the median of $BC$ is located on the origin $O$. The triangle has the following properties:

• $\angle ABC = 90^{\circ}$,
• $B=(r\cos(\alpha), t\sin(\alpha))$,
• $A=(-\sqrt{r^2\cos^2(\alpha) + t^2\sin^2(\alpha)},0)$,
• $C=(\sqrt{r^2\cos^2(\alpha) + t^2\sin^2(\alpha)},0)$,

where $\alpha = \angle BOC$ and $r,t$ some arbitrary real numbers.

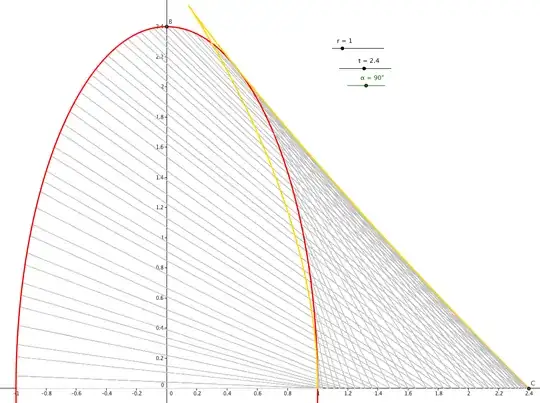
Now I am going to let Geogebra draw trace of the segments $\overline{AB}$ and $\overline{BC}$ while $\alpha$ changes from $0^\circ$ to $180^\circ$ for the following cases:

1. In this case $r=t=1$. Point $B$ changes location whereas the points $A$ and $C$ stay the same because

$$\sqrt{r^2\cos^2(\alpha) + t^2\sin^2(\alpha)}=\sqrt{r^2\cos^2(\alpha) + r^2\sin^2(\alpha)}=r$$

It can easily be verified that by interpolation the traces lead to a semi-circle of an area $\pi r^2/2$.

2. In this case $r=1$, $t=1.5$; as you can verify by the equations, the points $A,B,C, O$ change location. Particularly the point $B$ moves on an ellipse.

Finally, let's come to the problem:

I tried but couldn't calculate the area beneath the traces like the first case for the second case. How can I formulate the area? Any help is appreciated.

Answer 1

It is quite clear that the bell-shaped curve is formed by an arc of the ellipse of parametric equation $(r\cos\theta,t\sin\theta)$, traced by point $B$, and by an arc of the envelope of the family of lines $BC$ and $AB$.

In the following I'll assume $t\ge r$ and consider only the curve for $x\ge0$, as it is symmetrical around the $y$ axis. It is then enough to consider the envelope of lines $BC$.

The equations of lines $BC$ can be expressed as a function of $\alpha$ as $F(x,y,\alpha)=0$, where: $$ F(x,y,\alpha)= y\left(r \cos\alpha-\sqrt{r^2 \cos ^2\alpha +t^2 \sin ^2\alpha}\right)- t\sin\alpha\left(x-\sqrt{r^2 \cos ^2\alpha +t^2 \sin ^2\alpha}\right). $$ The equation of the envelope can be found from: $$ F(x,y,\alpha)={\partial\over\partial\alpha}F(x,y,\alpha)=0, $$ which give the parametric equations for the envelope: $$ \begin{align} x_{env}=& \frac{-r^3 \cos ^4\alpha+t^2 \sin ^2\alpha \cos\alpha \sqrt{r^2 \cos^2\alpha+t^2 \sin ^2\alpha}} {r \left(r \cos\alpha-\sqrt{r^2 \cos ^2\alpha +t^2 \sin ^2\alpha}\right)}+\\ &+\frac{r^2 \cos ^3\alpha\sqrt{r^2 \cos ^2\alpha +t^2 \sin ^2\alpha} -r t^2 \sin ^4\alpha-2 r t^2 \sin ^2\alpha \cos^2\alpha} {r \left(r \cos\alpha-\sqrt{r^2 \cos ^2\alpha +t^2 \sin ^2\alpha}\right)},\\ y_{env}=&\frac{t \sin ^3\alpha \cos\alpha \left(r^2-t^2\right)} {r \left(r\cos\alpha-\sqrt{r^2 \cos^2\alpha+t^2 \sin ^2\alpha}\right)}.\\ \end{align} $$

I represented in the picture below the region (gray lines) swept by segment $BC$, for $r=1$ and $t=2.4$. The red curve is the ellipse, while the yellow curve is the envelope found above.

The envelope has a cusp, located at $\alpha=\alpha_0\approx\pi/4$. We are interested in its outer part, corresponding to $\alpha_0\le\alpha\le\pi/2$. This part of the envelope meets the ellipse at a point $P$: the corresponding value of $\alpha$ can be found from the equation $(x_{env}/r)^2+(y_{env}/t)^2=1$. This has only one solution $\bar\alpha$ in the interval $(\pi/4,\pi/2)$, given by: $$ \begin{cases} \displaystyle\bar\alpha= \arccos{t\over\sqrt{3r^2+t^2}}, &\text{for $r<t\le\sqrt3r$;}\\ \displaystyle\bar\alpha= \arccos{r\over\sqrt{t^2-r^2}}, &\text{for $t\ge\sqrt3r$.}\\ \end{cases} $$

The corresponding values $\bar\theta$ for the parameter of the ellipse can be easily computed from: $\bar\theta=\arcsin(y_{env}(\bar\alpha)/t)$.

We can then represent half the area under the bell-shaped curve as an integral: $$ {1\over2}Area=\int_0^t y\,dx= \int_{\pi/2}^{\bar\theta}t\sin\theta{d\over d\theta}(r\cos\theta)\,d\theta+ \int_{\bar\alpha}^{\pi/2} y_{env}{dx_{env}\over d\alpha}\,d\alpha. $$

The first integral is easy to compute, but the second one is not and I suspect it cannot be expressed in elementary form. For $r=1$ and $t=1.5$ these integrals can be evaluated to $1.09117$ and $0.245874$, so that $Area=2.75247$.