I want to solve the following problem. It is not a homework.
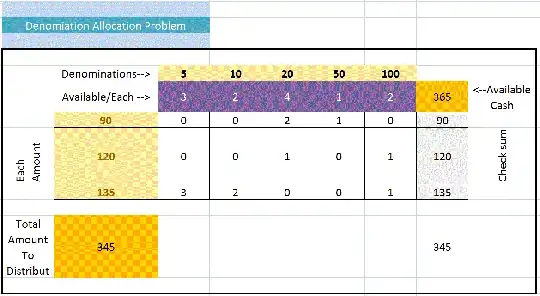
Assume that a company pays payroll to employees every period, the sum of the salaries for period is $T$. The accountant goes to the bank and withdraws the amount. She does not know what denominations she should ask the cashier to give here so that she can satisfy all salaries without asking any employee for change back. In the example below the denominations are 5,10,20,50 and 100. The total amount for all salaries for the period is 365. One employee gets 90 Dollars, the other gets 120 Dollars and the third gets 135 Dollars.
Questions:
Q1 - is to determine for each employee how many bills of each denomination to use so that the salary amount is paid in full and exactly without asking the employee to return change to the accountant. The answer presented suggests that first employee be paid 2-Twenty Dollars bill and 1-Fifty Dollars bill, and so on. Of course there may be 0, 1 or many solutions.
I am looking for the algorithm to use. You can help me by providing a reference instead of typing all the details.
Q2 - How can I tell if there is no solution?
Q3 - What area of mathematics study this kind of problem? Is it Dynamic Programming/Linear Programming?
Q4 - Do you know of any software that solves this kind of problems?
Thank you all.