5

The Problem

On an infinite plane there are two points, $A$ and $B$, a unit distance apart. There is a $50\%$ probability that there is an invisible wall somewhere between the two points. The wall extends $1/3$ unit in each direction perpendicular to the line between $A$ and $B$, and its position is uniformly distributed between the two points. You don't know if the wall is present or where it is until you run into it.

What strategy minimizes the expected distance to travel to point $B$ from point $A$?

(This problem originally came from Puzzling.SE but was closed for being "too mathy.")

My Solution

I use an $x$/$y$ coordinate system on the plane with the origin at $A$, and $B$ on the positive $x$-axis.

Once the position of the wall is known (i.e. when you run into the wall) the best strategy is to walk straight along the wall to the nearest end, then travel straight to $B$. The best strategy should therefore be to follow a fixed path from $A$ to $B$ until you reach $B$ or hit the wall; if you hit the wall, follow the previously stated path around the wall.

I break up the fixed part of the path into a number of small segments. A given segment covers a horizontal distance $\delta x$ and vertical distance $\delta y$. The length of each segment is weighted by the probability it gets traveled, which is $\frac{1}{2} + \frac{1}{2}\left(1-x\right)$. We also consider the probability that you have to walk around the wall, which for a given segment is $\frac{1}{2}\delta x$. The distance it takes to get around the wall is just $(H-y) + \sqrt{H^2 + (1-x)^2}$, where $H=\frac{1}{3}$, the half-length of the wall.

Therefore the expected distance $E$ should be equal to:

$$ E = \sum_{i=1}^N\frac{2-x}{2}\sqrt{\delta x_i^2 + \delta y_i^2} + \frac{\delta x_i}{2}\left((H-y_i) + \sqrt{H^2 + (1 - x_i)^2}\right) $$

If we treat $y$ as a function of $x$ (assuming that the optimal path doesn't travel backward) we can factor out $\delta x$, since $\delta y = y'(x)\delta x$; then taking the limit as $\delta x\to 0$ we obtain an integral:

$$ E = \frac{1}{2}\int_{0}^{1}(2 - x)\sqrt{1 + y'(x)^2} + H - y(x) + \sqrt{H^2 + (1-x)^2}~\mathrm{d}x $$

Now I try to use the Euler-Lagrange equations to find the path $y(x)$ that minimizes $E$:

$$ E = \int \mathcal{L}(x, y(x), y'(x))~\mathrm{d}x \\ \mathcal{L}(x, y(x), y'(x)) = \frac{1}{2}\left((2 - x)\sqrt{1 + y'(x)^2} + H - y(x) + \sqrt{H^2 + (1-x)^2}\right) \\ \frac{\partial \mathcal{L}}{\partial y(x)} - \frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial \mathcal{L}}{\partial y'(x)} = 0 \\ \left[-\frac{1}{2}\right]-\frac{\mathrm{d}}{\mathrm{d}x}\left[\frac{(2-x)y'(x)}{2\sqrt{1+y'(x)^2}}\right]=0 \\ 1 = \frac{y'(x)(1 + y'(x)^2) - (2-x)y''(x)}{\left(1+y'(x)^2\right)^{3/2}} \\ y''(x) = \left(1+y'(x)^2\right)\frac{y'(x)-\sqrt{1+y'(x)^2}}{2-x} $$

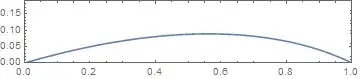
A solution to this differential equation should be a minimum-distance path, as long as it satisfies $y(x) \le H$ for all $x\in[0,1]$. The boundary conditions are $y(0)=y(1)=0$. Mathematica finds an explicit solution, but it it is extremely complex. The simplest form I can get it in is:

$$ y(x) = \frac{168 \left(9 \sqrt{6}+\sqrt{38}\right) \xi -\sqrt{131-9 \sqrt{57}} \xi^3 - 448 \sqrt{3710+378\sqrt{57}}}{2688 \left(27+\sqrt{57}\right)} \\ \xi = \sqrt{7 \left(43+\sqrt{57}\right)-8 \left(27+\sqrt{57}\right) x} \\ y(x) \approx 0.3929 x\sqrt{1.2802-x} +0.3454 \sqrt{1.2802-x}-0.3908 $$

The solution looks like this:

enter image description here

The Question

Is this approach valid, and are my calculations correct?

Community
  • 1
2012rcampion
  • 573
  • Interesting. What's the length of that path? – lulu Apr 16 '16 at 09:48
  • @lulu I can't integrate it symbolically (or rather, I can't persuade Mathematica to do it), but it's about 1.2161 units. (Compare this to the naive solution of staying on the centerline unless you're going around the wall, which has an expected distance of 1.3333...; not much improvement.) – 2012rcampion Apr 16 '16 at 09:50
  • 2
    It's worse than that....I'd say the naive solution was to go straight as long as I can, then if I hit the wall, climb up it and then go in a straight line to $B$. If I did that properly, the expected length of that path is $1.2307$. So you are talking about a very marginal gain...but a gain nonetheless. – lulu Apr 16 '16 at 10:00
  • Your approach looks sensible, and the answer seems plausible enough. I absolutely don't see any easy way to approach it. It's a good question...looks like the curve ought to have some natural, geometric meaning. – lulu Apr 16 '16 at 10:02
  • An (unachievable) lower bound on all strategies is when we have perfect knowledge of existence and location of the wall, in which case the expected travel distance is $1.12807$. Comparing to Lulu's achievable value of 1.2307, there is only a small wiggle room for optimization. – Michael Apr 16 '16 at 10:48
  • @2012rcampion : I do not see how your equations are incorporating the fact that the conditional probability of having a wall changes as we go further along the path. The conditional probability the wall exists, given we have already traveled $x$ units horizontally along the line, is $(1-x)/(2-x)$. – Michael Apr 16 '16 at 10:51
  • What is the source of this problem? It just appeared again, from a different user...the duplicate was deleted the moment I asked about the source. Is it from an active competition? – lulu Apr 16 '16 at 13:57
  • I originally asked this question on the puzzle site but it got put on hold. It is a variation of a puzzle posted on YouTube by Presh Talwalker. His had a fixed obstruction at the midway point between A and B. Mine has a randomly placed obstruction so the solution may be quite different. – David Apr 16 '16 at 14:00
  • @2012rcampion - You took my question from the puzzle site and posted it here and are now getting credit for it but it was my original question. – David Apr 16 '16 at 14:09
  • @David Here I'm specifically asking about whether my solution is correct (since I'm actually not that confidant in it); I thought this would be OK seeing as it looks like the question on Puzzling.SE will be closed, or at least put on hold indefinitely. As for the reputation, if you'd like I can ask a moderator to change this to a community wiki post so that I stop getting reputation from it, or I can delete it to remove any reputation I've gotten so far: which do you prefer? – 2012rcampion Apr 16 '16 at 14:26
  • You could have asked me to post it here so I get credit for it then edit the question to your better wording, then post your answer and ask people if it is correct. I also posted what I think is a possible near optimal answer but it involves computer simulation which I haven't done yet other the case where I walk straight towards B and then just walk around the wall and then directly at B. Using the $3$ mile AB path with $1$ mile detour (wall) I get $4.3836$ miles using about $300$ possible wall positions equally spaced (at $0.01$ miles , $0.02$... $2.99$). – David Apr 16 '16 at 14:32
  • @David My question isn't "come up with another way of getting the solution," it's "is my solution method valid?" If you want to ask about the solution in general, I think that should be a different question. – 2012rcampion Apr 16 '16 at 14:35
  • I am just upset that you took my problem and are getting points for asking it when you should have allowed me to post it here on this site. You basically copied my question and just twisted it to ask if your answer is correct. That is not nice at minimum and maybe against some rules. Don't do this in the future please it creates a "mess". – David Apr 16 '16 at 14:37
  • @2012rcampion - Should we delete this whole thing and start over? I will copy your wording of the question, posting it under my name, and let you post your answer and ask if it is correct and basically other people that answer my question will help confirm if your answer is correct or not. – David Apr 16 '16 at 14:40
  • 1
    @David Please don't copy my wording. From looking over your solution, it's apparent that we're talking about different variations of the problem, so you should ask about your variant. – 2012rcampion Apr 16 '16 at 14:42
  • @David I've flagged this question for a moderator to delete. Let me know when you post your question so I can also flag this one as a duplicate (to hopefully get it closed faster). – 2012rcampion Apr 16 '16 at 14:46
  • I reposted the question using the 3 mile distance and 1 mile detour constants but a variable position wall. – David Apr 16 '16 at 14:48
  • @David : I don't think 2012campion intended to steal your problem. I think 2012 appreciated your problem, but recognized that it was being marginalized on the original puzzle site. So 2012 posted it here, cited the source, and asked for feedback on an answer. That seems legit. On the other hand, your suggestion "I will copy your wording of the question, posting it under my name, and let you post your answer..." seems sketchy. Not a good idea to copy someone's words as if they were your own. – Michael Apr 16 '16 at 18:03
  • @Michael: I 100% agree; but I've been having a bad week, and ending it by arguing with someone on the internet would have just made me die inside. So, I just gave up as fast as possible. That's just how it goes sometimes... – 2012rcampion Apr 17 '16 at 00:45
  • You could avoid $y''(x)$ after the EL equation by integrating $1/2$. – Empy2 Apr 17 '16 at 02:55

2 Answers2

1

One approach is via dynamic programming (which works the solution backwards). For simplicity, let's chop the $x$-axis into $n$ segments of size $\delta_x = 1/n$, and suppose the wall is on one of these chopping points (including point 0, but not point 1). Chop the $y$-axis into $n$ segments of length $\delta_y = (1/3)/n$. Define the value function $J(x,y)$ as the expected remaining travel distance to the destination under the optimal policy, given we are at a horizontal distance $x$, a vertical distance $y$, and none of our previous moves encountered a wall. The $J(x,y)$ function is defined over: $$ x \in \mathcal{X} = \{0, \delta_x, 2\delta_x, ..., 1\} \quad , \quad y \in \mathcal{Y}=\{0, \delta_y, 2\delta_y, ..., 1/3\}$$

Suppose we start at $(x_0,y_0)=(0,0)$. Working backwards, and assuming there is no wall at $x=1$, we get:

$$J(1,y) = y \quad \forall y \in \mathcal{Y} $$

Now assume $J(k\delta_x, y)$ is known for all $y$ and for some $k$. Then:

\begin{align} J((k-1)\delta_x, y) &= P[\mbox{wall is here | have not yet seen it}]\left[1/3-y + \sqrt{1/9+ (1-(k-1)\delta_x)^2}\right]\\ &+P[\mbox{wall is not here | have not yet seen it}]\min_{v\in\mathcal{Y}}\left[J(k\delta_x,v)+\sqrt{\delta_x^2 +(y-v)^2} \right] \end{align} Since we have discretized the problem, if a wall exists then it is located uniformly over one of the the $n$ points $\{0, \delta_x, ..., (n-1)\delta_x\}$. Thus, if we are at location $(k-1)\delta_x$ and have not yet seen a wall at any of the locations $\{0, \delta_x, ..., (k-2)\delta_x\}$, we get: $$ P[\mbox{Wall here | not before}]=\frac{\frac{1}{2n} }{\frac{1}{2}+\frac{1}{2}\left(\frac{n-(k-1)}{n}\right)} $$

Michael
  • 26,378
  • I would suspect a near optimal solution would be to walk from A at an angle such that if the wall is at the $1.5$ mile marker you will hit the wall halfway up (or down) which is $0.5$ miles above (or below) the centerline (the direct AB path). If you don't hit the wall by then , then gradually lower your angle (or aim straight towards B), anticipting that the wall will NOT be there. The shape of your path after the $1.5$ mile marker might be a straight line segment towards B or a curved path to it (based on the probability of the wall being there). This is assuming direct AB path is $3$ miles. – David Apr 16 '16 at 14:12
  • Also, this might not be an easy problem to simulate on a computer. Question is what do you do as you pass the midpoint between A and B and haven't yet seen the wall? Do you then go straight at B, curve down slightly towards B and if so how much, or just hold your course? How would someone simulate all these variations to find the minimal path? How would they know for sure if they found the minimal path? – David Apr 16 '16 at 14:14
  • @David : It is pretty easy to run the above on a computer to recursively find the $J(x,y)$ values, although it seems to be an $O(n^3)$ algorithm and $n$ needs to be large for the discretized problem to be close to the continuous problem. – Michael Apr 16 '16 at 17:51
  • Once you have the $J(x,y)$ values, at every step $(k-1)$ where you are in location $(x[k-1],y[k-1])$ (where $x[k-1]=(k-1)\delta_x$), you observe whether or not there is a wall: If yes, do the optimal wall ending. If no, you move in a straight line to the point $(x[k],y[k])$, where $x[k]=k\delta_x$ and where $$y[k]= \arg\min_{v\in \mathcal{Y}}\left[J(k\delta_x,v) + \sqrt{\delta_x^2+(y[k-1]-v)^2}\right]$$ – Michael Apr 16 '16 at 17:51
  • This seems to give an optimal trajectory that is a trapezoid, see my more detailed answer here: http://math.stackexchange.com/questions/1745083/what-is-the-optimal-path-between-2-fixed-points-around-an-invisible-obstructin – Michael Apr 16 '16 at 22:24
  • Not so easy to run a recursive program here. The language I am using has restrictions on recursive depth. I have an algorithm in mind and presented it here in the comments, but even if I get it to work, I have no way of proving it is optimal. Is this one of those problems where someone says they got what they think is optimal then someone beats it slightly then a 3rd person beats that slightly or is there some way to definitively say an answer is optimal? – David Apr 16 '16 at 22:35
  • The above dynamic programming algorithm is optimal under the discretized model specified above, although it is only a numerical procedure (not as nice as a closed form formula). Intuitively, it should give a good approximation to the continuous model. I can send you the C program I used if you like, or include it in a verbatim mode. PS: I see another "Michael" is interested in this problem. – Michael Apr 18 '16 at 17:34
-1

My solution to this problem (which I originally posted on the puzzle site), would be to aim for the midpoint up the wall assuming it is midway between A and B. After that, I would lower my path back towards the centerline of A and B. I would have to use a computer to try many different paths and lowering angles. For example, if I don't hit the wall by midway between A and B, I could try going directly at B but this seems non optimal cuz think of the worst case where the wall is slightly before B. You then get diverted quite a bit just to finish a small distance to B. I think a simple and near optimal solution would be after not seeing the wall by the midpoint of the direct AB path, plot a few more discrete points that the wall could be at (such as $5/8$th of the way, $3/4$s of the way, $7/8$ths of the way), optimize just those paths, then find a formula that passes thru those $3$ points (called curve smoothing I think?). Not sure if that will be optimal for all wall positions past the halfway point but it is a good start to try to beat.

David
  • 1,710