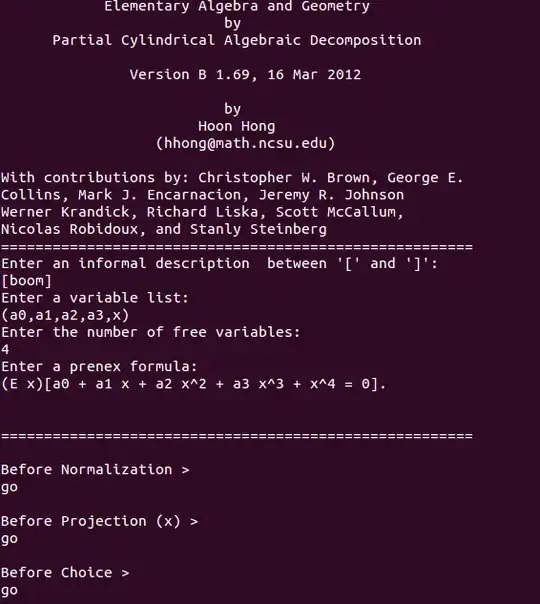
I wanted to find the semialgebraic set in the $(a_0,a_1,a_2,a_3)$ space that guarantees that there exists at least one real root of the general polynomial equation of degree 4. For that purpose, installing QEPCAD on Ubuntu 14, I tried to eliminate the only existential quantifier in
$\exists x[x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0 = 0]$
Giving successive input as
made QEPCAD think for several minutes, and then fail, due to lack of memory I suppose (actually a similar problem is among the examples on QEPCAD site, http://www.usna.edu/CS/qepcadweb/B/examples/Quartic/Quartic.html, but even increasing, for that problem, the +N from the default value to +N80000000, did not help).
Now the complexity of the known quantifier elimination algorithms, according to http://mathworld.wolfram.com/QuantifierElimination.html for example, is bad (doubly exponential asymptotically, at least in the number of quantifiers alternations), but I thought that for such simply looking problem, the answer would be obtained nevertheless relatively quickly.
So, is the situation with these algorithms is really that bad from a practical point of view? Looking for reference on practical implementation issues, I found that some speak of "applications in industry" (e.g. http://www.issac-symposium.org/2014/tutorials/ISSAC2014_tutorial_handout_Anai.pdf), but the examples brought in the text (superficially looking through the text) seemed not that much more complicated than the one above.
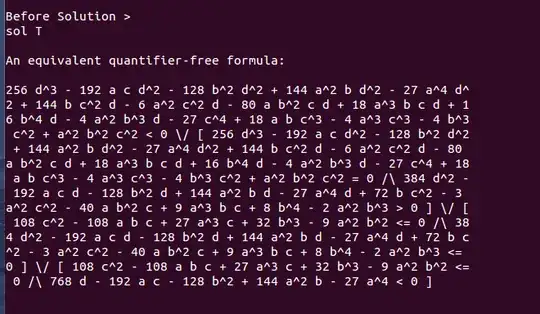
EDIT: there was maybe some environment issue, or an issue with the precise syntax I used, though I did not get any error message regarding syntax, or another mistake I made (I will try to understand what happened, and then edit the question again). Right now I got, after very little time, eliminating quantifiers from
$\exists x[x^4 + a x^3 + b x^2 + c x + d = 0]$
EDIT:
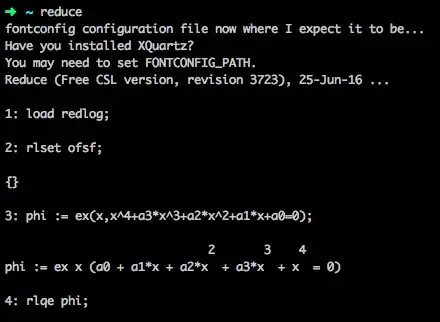
well, things are more complicated.. First, the program QEPCAD is interactive, and the user apparently can specify different options on the command line at various stages of searching for a solution. I could not find the documentation of these options on QEPCAD site (perhaps I did not search well enough). Second, the ability of QEPCAD to eliminate quantifiers in the formula I specified depends on variable names (which means probably that it depends on variables order, http://staff.bath.ac.uk/masjhd/ISSACs/ISSAC07-final.pdf ), so while $\exists x[x^4 + a x^3 + b x^2 + c x + d = 0]$ was solved in 1 second or so, but $\exists x[x^4 + d x^3 + c x^2 + b x + a = 0]$ was not (I am still waiting for the solution to come out, that is, afer having inserted "go" on the command line whenever interactive input was expected).
It looks like a considerable effort was invested in QEPCAD, but as it is, it is difficult to use by a non expert (and I did not find any detailed documentation). I wonder whether there is commercial software which is substantially better (and by the way which is that commercial software? MAPLE?)