4

For any two points on a hexagonal grid with integer coordinates there is a unique parallelogram which contains all of the shortest paths (in terms of taxicab norm) between these points. See the picture:

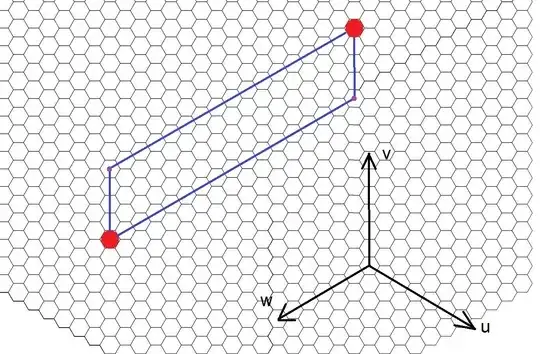
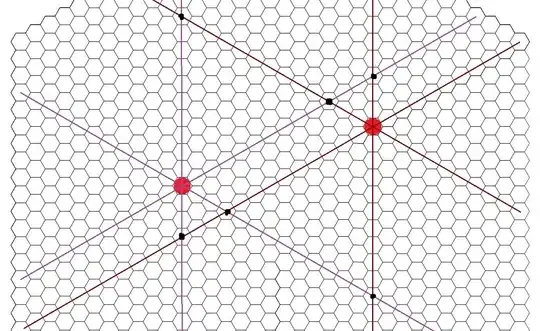
enter image description here

Knowing the coordinates of both points in a hexagonal system $(u_1,v_1,w_1)$ and $(u_2,v_2,w_2)$, how do we find other two vertices of the parallelogram? I mean the general formula.

On the rectangular grid it's very simple. We just switch the coordinates to get the rectangle containing all shortest taxicab paths:

$$(x_1,y_1)~~(x_2,y_2)$$

$$(x_1,y_2)~~(x_2,y_1)$$

What do I know about this parallelogram on a hexagonal grid:

  • Its angles are $\pi/3$ and $2 \pi/3$
  • Its larger diagonal length is equal to the Euclidean distance between the points:

$$d=\sqrt{a^2+b^2+c^2-ab-ac-bc}$$

With $a=u_1-u_2$, $b=v_1-v_2$, $c=w_1-w_2$.

I accept any convention for hexagonal coordinates, as long as it solves the problem.

The coordinates I use are explained in detail in this question.

Edit

As for the explanation why we need three coordinate axes, see this picture:

enter image description here

There are $6$ intersection points in general, but we need to find the two which are closest to the line, connecting the original points. The intersection points are:

$$(u_1,v_2,0)$$

$$(u_2,v_1,0)$$

$$(u_1,0,w_2)$$

$$(u_2,0,w_1)$$

$$(0,v_1,w_2)$$

$$(0,v_2,w_1)$$

This is why this problem is trivial for rectangular lattice (only two intersection points), but more complicated for hexagonal lattice (six intersection points).

How do I choose the correct two points which define the smallest parallelogram?

Community
  • 1
Yuriy S
  • 32,728
  • Are these coordinates even unique? It seems that $(1,1,0)=(0,0,-1)$ i.e. in your diagram if one starts at the origin of the suggested 3 coordinates indicated by the three black segments, and then goes 1 unit in each of the u and v directions, one arrives at the hexagon which is "up and right" and adjacent to the hexagon containing the origin (so that could be called $(1,1,0).$. But another way to get there is to face in the w direction and go backward one step, i.e. $(0,0,-1).$ – coffeemath Apr 06 '16 at 01:58
  • @coffeemath, No, the coordinates are not unique, up to the addition of $(p,p,p)$ for any integer $p$. The distance $d$ stays the same – Yuriy S Apr 06 '16 at 05:39
  • If three coodinates are used, how is the taxicab distance to be defined? – coffeemath Apr 06 '16 at 11:45
  • @coffeemath, to clarify - the taxicab distance is precisely the smallest number of steps we need to take to get from one point to another. There can be no confusion about it even with three coordinates – Yuriy S Apr 06 '16 at 11:56
  • It isn't clear (to me) that if $d(A,B)$ is the smallest number of steps to get from $A$ to $B,$ that this distance function satisfies the triangle inequality. (I don't know if that matters for what you're doing.) Also does one restrict to points $A,B$ whose coordinates in the $x,y,z$ system are all integers? – coffeemath Apr 06 '16 at 12:24
  • 1
    @coffeemath, it doesn't matter about triangle inequality. As for the other question, I only consider points with integer coordinates in $u,v,w$ system, not in the cartesian system – Yuriy S Apr 06 '16 at 12:28
  • Let us continue this discussion in chat. – coffeemath Apr 06 '16 at 12:41
  • somewhat related (and currently bountied): Determine if a coincident point in a pair of rotated hexagonal lattices is closest to the origin – uhoh Jun 07 '20 at 05:57

1 Answers1

2

The following is an attempt to describe how to obtain the "other vertices" of the parallelogram in order to see how to get the least lattice-step distances.

Let $P,Q$ be two points on the lattice which we desire to complete to a parallelogram, in such a way that moving along edges from $P $ to $Q$ gives the shortest path in lattice moves. There is no loss if we take $P=(0,0,0),$ and $Q=(a,b,c)$ may by use of addition/subtraction of $(t,t,t)$ be put into its unique form with one coordinate zero and the other two nonnegative. In what follows all triples will be assumed to be in this unique form. [This is the format used in the OP's previous post, linked to in this post.]

There are six rays from the origin which cut the plane into six parts, and the locations of the other two points of the determined parallelogram depend on in which of these regions $Q$ lies in. The rays, going around clockwise from the positive x axis, are the sets of points (with $k>0$) $$(k,0,0),\ (k,k,0),\ (0,k,0),\ (0,k,k),\ (0,0,k),\ (k,0,k)$$ These are, respectively, the positive x, negative z, positive y, negative x, positive z, and negative y axes. These names are natural, since for example $(k,k,0)=(0,0,-k), $ making the second one in the list appropriately termed the negative z axis. Note first that if $Q$ happens to be on one of the above six rays ("on an axis") then the parallelogram will be degenerate (so no need to express the other vertices of the parallelogram), so we can assume the coordinates of $Q$ always consist of one which is zero, and the other two are two distinct positive integers. Now whichever two rays $Q$ lies between, the other two points of the parallelogram should lie on those two lines, and reached by appropriate projections in one of the littice direction. This will in each case give two-leg journeys from the origin (recall we took that as $P$) to the point $Q$ (go along one bounding ray, then directly to $Q$ in a direction determined by the other bounding ray). For example consider the rays $(k,0,0)$ and $(k,k,0)$ which are the bounding rays for the region contining $(a,b,0)$ when $a>b>0.$ Then the other two points of the parallelogram are $(a-b,0,0)$ and $(b,b,0).$ A move from the origin to $(b,b,0)$ takes only $b$ moves, since we are moving along the negative $z$ axis a total of $b$ steps. Then from there to $(a,b,0)$ takes an additional $a-b$ moves, this time the movement being along the $x$ axis.

Besides the above case there are five others, summarized below. $$(a,b,0),\ b>a:\ \ (a,a,0),\ (0,b-a,0). \\ (0,b,c),\ b>c:\ \ (0,b-c,0),\ (0,c,c). \\ (0,b,c),\ c>b:\ \ (0,0,c-b),\ (0,b,b). \\ (a,0,c),\ c<a:\ \ (0,0,c-a0,\ (a,0,a). \\ (a,0,c),\ a>c:\ \ (a-c,0,0),\ (c,0,c). $$ For each of these it is assumed $a,b>0$ and unequal, as specified in the cases. The two triples to the right of the case are then the unique addresses of the other two vertices of the parallelogram in that case.

A summary of the cases: In each one, $Q$ is a triple $(u,v,0)$ with $u>v,$ where this triple is in all but one case not listed in the $(x,y,z)$ order of the original system of coordinates. One of the other vertices of the parallelogram is $(v,v,0)$ reached from $Q$ by moving $u-v$ units in the direction of the positive first coordinate. The other vertex is $(u-v,0,0)$ reached from $Q$ by moving $v$ units in the negative third coordinate direction (i.e. by subtracting a multiple of $(1,1,0)=(0,0,-1.).$ Totalling the steps gives $(u-v)+v=u$ steps in going from the origin to $Q.$ This gives the simple summary method for getting the number of steps from the origin to $Q,$ namely express $Q$ in the unique form with one coordinate zero and the other two non-negative, and then the number of steps required is the maximum coordinate value of that expression for $Q.$

I have not proved that in all cases this gives the minimal stepwise distance, but in examples I've looked at it seems it does.

coffeemath
  • 30,190
  • 2
  • 34
  • 53