11

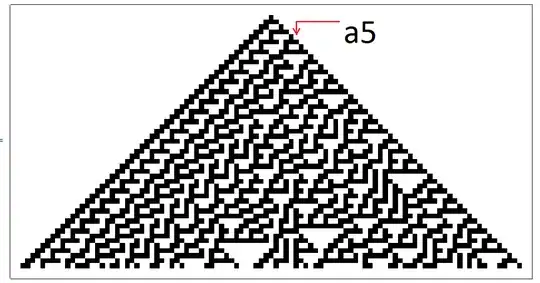
If we consider a simple 1D cellular automaton (acting on a binary string) and record a value at a fixed position in the string, we can interpret the recorded sequence as a binary number.

Most simple deterministic cellular automata generate periodic sequences of binary digits which can be interpreted as rational numbers.

However, there are 'random' deterministic CA, such as elementary CA rule 30, discovered by S. Wolfram. Starting from a single point, it generates data which is random enough to be used as a random number generator. See this paper for more information.

Now, since this CA has perfectly deterministic (and simple) rules, what can we tell about numbers it generates at fixed string positions?

Since most of the 'randomness' happens to the right side, let's look at the numbers we get at positions from the center to the right, starting from the topmost $1$ in each case (see the figure). All the numbers are considered to have zero integer parts and are converted to the decimal notation from binary:

$$a_0=0.8623897839473840486408002460867511281\dots$$

$$a_1=0.6619938131535679545367590611375473724\dots$$

$$a_2=0.7759963493462055882598583123808285092\dots$$

$$a_3=0.7313593429560050953478343145780694591\dots$$

$$a_4=0.8215879687059052475349289186091204860\dots$$

$$a_5=0.6314259431664999548181068438831291123\dots$$

$$a_6=0.8079966728503828647993510584534608703\dots$$

enter image description here

Can we prove/disprove that these numbers are irrational? Trancendental? Or can we only guess based on direct experiments? What about other such 'random' cellular automata?

Yuriy S
  • 32,728
  • Unless you don't have infinite digits your number is rational. And you can only have infinite digits in infinite time. – N74 Apr 04 '16 at 22:57
  • @N74 Yes, but cellular automata like this continue forever. The OP has just shown the first few steps. With each new step, you get more digits. –  Apr 05 '16 at 00:02
  • @N74, are you saying that irrational numbers don't exist? No one was able to obtain infinite digits of $\pi$ yet – Yuriy S Apr 05 '16 at 05:39
  • @YuriyS I'm saying that no deterministic process can generate an irrational number, unless it runs forever. Think about the classical example of the construction of an irrational number: $a_0=0.1$, $a_1=0.101$, $a_2=0.101001$, $a_3=0.1010010001$; $a_{\infty}$ is trascendental but all $a_n$ are rational. – N74 Apr 05 '16 at 07:04
  • @barrycarter Irrational numbers should have a countable infinity of digits, let the algorithm run and, at the end of the universe, you will have an irrational number. No machine-representable number is irrational. – N74 Apr 05 '16 at 07:09
  • @N74, again, are you saying that $\pi$, $e$, $\sqrt{2}$, etc, don't exist? Why can't a Cauchy sequence be defined by a cellular automaton (or other machine)? – Yuriy S Apr 05 '16 at 07:48
  • @YuriyS because of time and resources: no machine have no limitation on both. – N74 Apr 05 '16 at 08:05
  • @N74, I'm sorry, could you please clarify your position about irrational numbers in general? Do they exist even though we can't compute them in a finite amount of time? – Yuriy S Apr 05 '16 at 08:18
  • @YuriyS For sure irrationals do exist and we have plenty of evidence of this in our continuous world. The problem is to generate them into a machine... without infinite memory you are bound to repeat the sequence, first or last. – N74 Apr 05 '16 at 08:53
  • To resolve this, can we say we have a sequence of computable rational numbers whose limit converges to an irrational number? –  Apr 05 '16 at 13:05
  • the point is this, no deterministic finite automaton can generate irrational numbers. – jimjim Apr 24 '16 at 10:41
  • @Arjang, then there is no way to generate irrational numbers at all? – Yuriy S Apr 24 '16 at 10:43
  • @YuriyS : sure there is, take for example binary digits being 0.10110011100011110000.... thats an irrational number, maybe even transcendental. the digits are easy to generate, as long as they are not repeating from some points onwards. – jimjim Apr 24 '16 at 10:58
  • @YuriyS : I just made up that number, you can learn more about numbers like that from this link http://mathworld.wolfram.com/LiouvillesConstant.html – jimjim Apr 24 '16 at 11:06
  • @Arjang, but that's a deterministic process, isn't it? And by the way, what do you meant by 'finite automaton'? Any process we (as humanity) have ever done is finite – Yuriy S Apr 24 '16 at 11:58
  • @YuriyS : deterministic process is not same as determinitic Finite state mchine, and yes not only what you said is true also the entire universe is not enough to represent all digits of square root of two. you might want too look at limits of computation, the omega number and orders of infinity. – jimjim Apr 24 '16 at 12:07
  • @Arjang, we can prove that $\sqrt{2}, e, \pi$ are irrational, despite the fact that any decimal expansion of them we ever created is a rational approximation. The numbers I ask about meant to be taken as a limit going to infinity assuming we continue to generate the CA – Yuriy S Apr 24 '16 at 12:20
  • @YuriyS : I am sorry, maybe I am missing something here. Any number with random digits is irrational for sure. Ill reread the question to understand the question. – jimjim Apr 24 '16 at 12:26
  • I am not sure what you are asking, but philosophically natural numbers do not exist in our universe, their representations do. – jimjim Apr 26 '16 at 08:18
  • @Arjang, now that I think about it - my question is more 'what do we consider random'? See the paper I linked, maybe you will understand what I'm asking – Yuriy S Apr 26 '16 at 09:24
  • @N74 "For sure irrationals do exist and we have plenty of evidence of this in our continuous world. The problem is to generate them into a machine... without infinite memory you are bound to repeat the sequence, first or last." Let me remind you this is math. What you said concerns feasibility in reality. However, we both know how reliable a indicator feasibility is in predicting possibility. – Zach466920 Apr 27 '16 at 00:43
  • I need clarification on how you are you getting the $a_n$. For instance for $a_0$ you seem to start from the top at the center then create a binary number using the celluar automata for the values. Each value at the center is either $0$ or $1$. For instance the first row has $1$, then second has $1$ the third has $0$ and so on? – Zach466920 Apr 27 '16 at 00:45
  • @Zach466920, each number is created by taking cell values in a vertical column as 0 or 1. $a_0$ is a central column. You seem to understand correctly . If I was taking rows, each number would have finite expansion, i.e. be rational – Yuriy S Apr 27 '16 at 05:13

2 Answers2

4

The answer itself isn't very surprising or illuminating so sorry :/

First, since you've posted a picture of rule 30, discussed here, we will be considering number generation from that CA only.

Second, recall the definition of an irrational number,

An irrational number is a number that cannot be expressed as a fraction p/q for any integers p and q.

Corollary 1:

Irrational numbers have decimal expansions that neither terminate nor become periodic.

Proof: Assume that the decimal expansion does repeat. Then the number is, by definition, rational. Thus, our assumption is false, and the corollary is true.

Now it's been proven by Jen 1990 that with the initial state of a single black cell, the sequence of colors attained in any two adjacent cells is not periodic. Corroborated by Gray 2003.

So if we define a sequence of numbers using the cell states generated by rule 30, then the digits will not be periodic. By Corollary 1, If the digits are not periodic, then the number is irrational.

So let's look at your question(s)

Can we prove/disprove that these numbers are irrational?

We can prove that these numbers are irrational, for rule 30.

Trancendental?

Almost surely.

What about other such 'random' cellular automata?

Any cellular automata with non-periodic evolution will also generate irrational numbers.

Zach466920
  • 8,419
  • When you say "almost surely" I take it to mean it would be very surprising if any were algebraic. – DanielWainfleet Apr 28 '16 at 15:07
  • 1
    @user254665 Actually I mean it in the mathematical sense. Since rule 30 is also chaotic, the cells evolve in a pseudo random manner. Almost surely, such a number is transcendental. – Zach466920 Apr 28 '16 at 15:12
  • Small point: for Rule 30, while wildly unlikely, it remains an open question whether or not every infinite column never lapses into a cycle; it has been proven that at most one column can do this. If somehow there were a repeating column (there's absolutely not, but nobody can prove it), that column would be rational. – Trevor Aug 15 '22 at 18:43
2

While almost all real numbers are transcendental, it is devilishly difficult to prove it for specific real numbers, especially those given by their base $b$ expansion. (For those "natural" quantities for which a proof of transcendence is known, it is generally by viewing these quantities as particular values of special functions and using techniques from analysis on such functions.) Unlike irrationality (a number is irrational iff its base $b$ expansion is not eventually periodic), there is nothing analogous for transcendence.

Even for the very simple-looking Champernowne constant ($0.12345678910111213...$), it was difficult to prove its transcendence. You shouldn't expect a proof of transcendence of quantities whose base $b$ expansions are defined by cellular automata.

There is, however, a remarkable result that bears at least some resemblance to what you're asking for, at least in the sense that the keywords "automaton", "base $b$ expansion" and "transcendence" appear in it:

If $x$ is a real number (and $b\geq 2$ an integer) such that the base $b$ expansion of $x$ is not eventually periodic, and "$b$-automatic" in the sense that the $i$-th decimal of $x$ in base $b$ can be computed by a finite automaton from the base $b$ expansion of $i$ itself, then $x$ is transcendental.

A first "proof" appeared as: Loxton & van der Poorten, “Arithmetic properties of automata: regular sequences”, J. Reine Angew. Math. 392 (1988), 57–69; however, that paper contains a flaw. A correct proof, together with related results and conjectured, appeared much more recently: Adamczewski & Bugeaud, “On the complexity of algebraic numbers I. Expansions in integer bases”, Ann. of Math. 165 (2007), 547–565. (Here is a survey related to such questions, although it does not seem to be aware that the Loxton & van der Poorten paper is flawed.)

This result implies, for example, that the number whose binary expansion is the Morse-Thue sequence, viz., $0.01101001100101101001...$, is transcendental (because it is certainly automatic and non periodic). This is certainly the closest you will get to the sort of quantities you were asking about.

(Also remarkably, for formal power series over finite fields, there is a result due to Christol, Kamae, Mendès-France and Rauzy which says essentially the "opposite" of the one quoted above: the coefficients of the formal power series are automatic iff the power series is algebraic.)

Community
  • 1
Gro-Tsen
  • 6,251
  • 26
  • 64
  • I'm not sure why you're so pessimistic about proving that a cellular automata-generated number is transcendental, when you then immediately cite a very similar (and marvelous) result about how finite automata-generated numbers are transcendental. – Jack M Apr 29 '16 at 21:28
  • @JackM Because the theory of finite automata is extremely constrained and well-understood, and even then it turned out to be immensely difficult to prove the transcendence of the expansions they recognize; cellular automata can do pretty much anything, I think it's unreasonable to hope for transcendence results there (but of course, I'd be happy to be proved wrong!). – Gro-Tsen Apr 29 '16 at 21:51
  • @Gro-Tsen, thank you very much for your answer. I'm sorry, I couldn't reward you, but the other answer appears more relevant to me – Yuriy S May 01 '16 at 19:13
  • @Gro-Tsen I think there are two distinct questions here: 'given a CA, can we prove that any of the numbers it generates are transcendental?' and 'Can we exhibit a CA that generates transcendental numbers in such a fashion?' The answer to the first is likely to be as difficult as you say, but I think the answer to the second should be positive by translating over an appropriate construction. – Steven Stadnicki Jan 08 '20 at 21:19