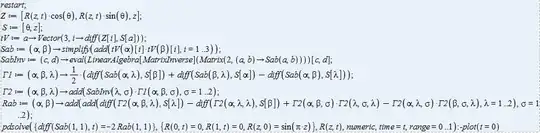I am trying to generate a Maple Simulation for Ricci Flow assuming general Solids of Revolution and such. I assume that there is a surface with the following parametrization: $$S:\left\{\begin{matrix}x=R(z,t)\cos\theta \\y=R(z,t)\sin\theta\\ z=z\end{matrix}\phantom{..}\begin{matrix}\theta\in[0..2\pi] \\ z\in[0..1]\end{matrix}\right.$$
And want to see how the surface is deformed by Ricci Flow. My Maple Code is as such:
-I define my x,y,&z coordinates
-I define the tangent vectors
-I define the metric tensor
-I define the Christoffel Symbols
-I define the Ricci Tensor
-I attempt at pdsolving the equation
$$\frac{\partial}{\partial t}g_{i j}=-2R_{i j}$$
Everything goes lovely, but upon the execution of the final line, I get the following message:
"Error, (in pdsolve/numeric/plot) unable to compute solution for t>HFloat(0.0): Newton iteration is not converging"
Can someone please help me as to the fail in the way I set up my Maple Code? Thanks a lot everyone.