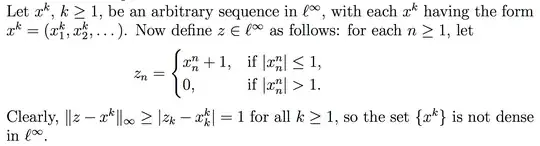4

I'm looking at the proof of showing that $l_\infty$ is not separable, but there is a minor detail I don't understand. In the proof below, is it necessary to define $z_n$ as such instead of simply defining $z_n=x_n^n +1$? I don't understand why we need to separate $z_n$ into two cases depending on the size of $|x_n^n|$, the proof seems to work out regardless.

enter image description here

nomadicmathematician
  • 6,309
  • 3
    It’s to ensure that $z$ is actually in $\ell^\infty$: it ensures that $|z|\le 2$. – Brian M. Scott Feb 25 '16 at 22:13
  • @BrianM.Scott What is the idea to define $z_n$? Is it started from $|z_n−x^n_n|≥1$ for every $n$? So, if we define $z_n=0$, then we have $|0−x_n^n|=|x_n^n|≥1$. And for $|x_n^n|<1$, we can define $z_n=x_n^n+1$ to make sure that $|z_n|=|z_n^n+1|≤|x_n^n|+1<1+1=2$ which implies $\sup_{n \in \mathbb{N}} |z_n|<\infty$. – user136524 Jan 09 '22 at 06:26
  • 1
    @MathLearner: Yes, the idea is to make $|z_n-x_n^n|\ge 1$ for each $n$, since that ensures that $|z-x^k|_\infty\ge 1$ for each $k$. And yes, you’ve correctly understood the rest of the argument. – Brian M. Scott Jan 09 '22 at 21:43

2 Answers2

4

Note that the sequence $\{x_n^n\}$ may be unbounded.

ajotatxe
  • 66,849
1

Another way to see non-separablity is to consider the uncountable set $S$ of binary sequences. That is, $(x_n)_n\in S\iff \forall n (x_n\in \{0,1\}).$ The family of non-empty open balls $\{B(s,1/2):s\in S\}$ is pair-wise disjoint and uncountable. A dense set must intersect each one of them.

DanielWainfleet
  • 59,529