Geometric Interpretation of Complex Algebraic Proof of Sum of Squares Statement

Question

When I see answers regarding proofs such as the one mentioned here, it seems that there is a considerable diversity of ways to attempt to look at this proof. Similarly, although this sum of squares question is very different, I was wondering if there was a geometric interpretation to the following problem:

Prove that given $ a,b,c,d \in \mathbb{Z} \ \ \Rightarrow \ \ \exists \ u,v, \in \mathbb{Z} \ \ s.t. $ $$ (a^{2} + b^{2})(c^{2} + d^{2}) = u^{2} + v^{2} $$

I have mentioned my solution to the problem using basic tools from my complex analysis class.

---

We write the statement as the product of complex conjugates to prove this theorem:

$ a^{2} + b^{2} = a^{2} - b^{2} (-1) = a^{2} - b^{2} i^{2} $
$ = a^{2} - (bi)^{2} = a^{2} - (ab) i + (ab) i - (bi)^{2} $
$ = a(a-bi) + bi (a-bi) $
$ = (a+bi)(a-bi) $

Similarly, we repeat the procedure for $c^{2} + d^{2}$ to get the expression:

$ (c+di)(c-di) $

Taking the product:

$ = [(a+ bi)(a- bi)] [(c+di)(c-di)]$
$ = [(a+bi)(c+di)][(a-bi)(c-di)] $

The numbers in both terms are complex conjugates So, we can express them in terms of $u$ and $v$. This gives us: $ (u+vi)(u-vi) $

$ \therefore u + vi = (a +bi)(c+di)$
$ \therefore a(c+di) + bi(c+di) $
$ \therefore (ac) + (ad)i + (bc)i + (bd)(i^{2}) $
$ \therefore (ac) + (ad)i + (bc)i + (bd)(-1) $
$ \therefore (ac - bd) + (ad + bc)i \equiv u + vi $

We we are left with expressions to determine u and v for all integers a,b,c,d.
$ u = ac - bd $
$ v = ad + bc $

These satisfy our original statement. For example:
$ (2^{2} + 3^{2})(4^{2} + 5^{2}) = (4+9)(16+25) = 533 $
$ u = (2)(4) - (3)(5) = 8 - 15 = -7 $
$ v = (2)(5) + (3)(4) = 10 + 12 = 22 $
$ u^{2} + v^{2} = (-7)^{2} + (22)^{2} = 533 $

---

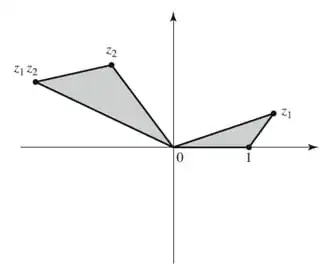
Note that during the process of this proof, we were taking products of two complex numbers. A geometric interpretation of that is shown below (reproduced from Complex Analysis. Bak, Newman). However, given that this is a number theoretic problem and the complex numbers cancel out to give integers, do complex numbers still help us give a geometric explanation?

Answer 1

The complex explanation of this doesn't depend on how the angles behave in complex multiplication. It is merely the observation that for complex numbers, $|wz| = |w||z|$, or by squaring, $|wz|^2$ = $|w|^2|z|^2$. Combine this with the fact that if two complex numbers have integers for both real and imaginary parts (such complex numbers are called Gaussian Integers), then so does their product, and you have the result.

To make this a geometric picture, then you need to explain both multiplying moduli and preservation of Gaussian Integers under multiplication geometrically. The picture you provided gives a geometric interpretation of how the arguments add when you multiply, but that isn't important here. It doesn't provide a good geometric understanding that the moduli multiply, which is what is needed.

I am not personally aware of a good way of showing that moduli multiply geometrically. Perhaps there is one, but personally I think you would be better off looking elsewhere for a strictly geometric interpretation of the proof.

Answer 2

I. Algebraic preliminaries. Laplace's Identity for 3D vectors $\vec V, \vec W$ states that cross products and dot products are related by $$(1) \qquad ||\vec V||^2\ ||\vec W||^2 = ||\vec V \times \vec W||^2 + ||\vec V \cdot \vec W||^2$$

It can be proved by brute force algebraically.

Specializing to the case that both vectors lie in the plane, by setting

$\vec V= <a,b,0>, \vec W=<c,d,0>$ proves what you wanted. In more detail, if $\vec V= <a,b,0>$ and $ \vec W= <c,d>$ we get $(a^2+ b^2)(c^2+d^2) = ||\vec V||^2 ||\vec W||^2 = $ sum of two squared terms, namely $||\vec V\cdot \vec W||^2 + ||\vec V \times \vec W||^2$. That's the algebraic method.

The algebraic structure of this identity (its scaling properties) makes it clear that if is true for unit-length vectors it must be true in general.

II. Geometric method. Now we can prove Laplace's Identity geometrically, at least in the special case where $V$ and $W$ are unit vectors. By the parallelogram law of vector addition, the points $0, V, W, V+W$ form the vertices of a rhombus, and the diagonals $ A=V-W$ and $B=V+W$ are therefore orthogonal vectors. (This orthogonality can be checked easily by taking the dot product of $A$ and $B$, checking that you get zero). Next solve for $V$ and $W$ in terms of two orthogonal components $A$ and $B$. For example, $V=\frac{1}{2} (A+B)$ After a rotation of space we can assume everything lies in the plane, and $A$ and $B$ are parallel to the $x$ and $y$ axes: $A=<a,0,0>, B= <0, b,0>$. Then $2V= <a,b,0> $ and $2W= <-a,b,0> $. Then you can verify fairly easily that the dot and cross products behave as desired.

III. Generalization to higher dimensions. The cross product of two vectors is not defined for vectors in higher dimensional Euclidean space (the cross product is no longer a vector). However there is a natural extension of the cross product to higher dimensions, called the wedge product $ \vec V\wedge \vec W$. (Basically it is collection of all ${{n}\choose {2}}$ possible $ 2\times 2$ sub determinants extracted from the $2\times n$ matrix whose two rows are $\vec V$ and $\vec W$.) Then Laplace's Identity states that $||\vec V||^2 ||\vec W||^2 = (\vec V\cdot \vec W)^2 + ||\vec V \wedge \vec W||^2$.