2

Consider the following game.

P has a fair $6$ sided die and continuously rolls it while keeping track of the sum, $S$, of the top faces. P can bail anytime and leave with $S$ number of dollars. However, if $S$ is ever a perfect square, the game ends and $P$ gets nothing.

When is it most profitable for $P$ to quit? What is the expected amount of money does $P$ make when $P$ quits at this optimal time?

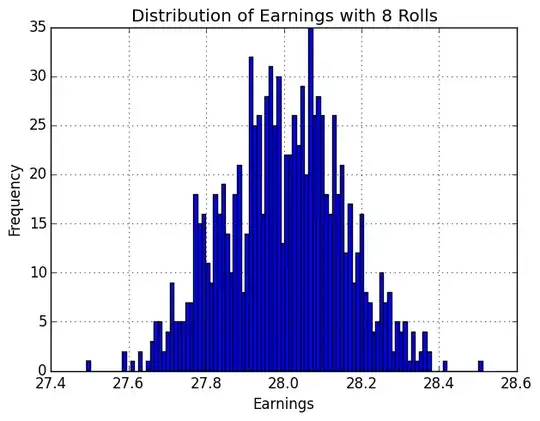
I ran sum simulations of this and found that on average, the game runs for $8$ rolls and the expected earnings of $P$ is around $28$ dollars. Can we prove this?

The distribution of earnings with $8$ rolls is shown below. enter image description here

Sandeep Silwal
  • 8,363
  • You'll want to quit only if you can "hit" a square. But as you (after a while) have the same probability to hit each square, and that the square are further and further away, I think there is no optimal time to quit. – Tryss Dec 11 '15 at 08:26
  • What's up with fractional earnings? – A.S. Dec 11 '15 at 08:52
  • 1
    You should not decide in advance how many rolls to attempt. Instead you should decide to quit when the sum hits particular values. – Henry Dec 11 '15 at 09:14
  • Related: http://math.stackexchange.com/questions/977679/toss-a-fair-die-until-the-cumulative-sum-is-a-perfect-square-expected-value and http://math.stackexchange.com/questions/1176195/would-you-ever-stop-rolling-the-die – Henry Dec 11 '15 at 09:16

0 Answers0