12

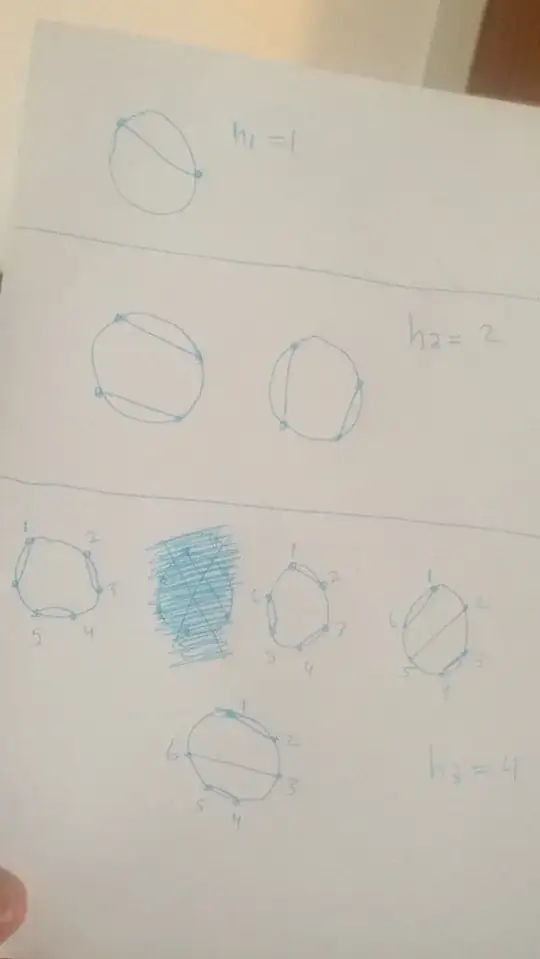
For $n \geq 0$ evenly distribute $2n$ points on the circumference of a circle, and label these point cyclically with the numbers $1, 2 . . . , 2n$ Let $h_n$ be the number of ways in which these $2n$ points can be paired off as $n$ chords where no two chords intersect

I want to find a recursive formula for $h_n$.

First I find $h_1,h_2,h_3$ to see the recursive nature.

enter image description here

$h_1 = 1$ as their only one way to make one chord

$h_2 = 2$

Now $\require{enclose} \enclose{horizontalstrike}{h_3=4}h_3=5$ ((1,4), (2,3), (5,6) case is missed in image)

I found a wikipedia link

Motzkin numbers and it is very close to my problem, But in this link you don't need to pair off $n$ chords.

But I can't get to come up with a recursive formula for my question.

If I would to guess I would say $h_n = 2 \times h_{n-1}$, And would this means that $h_4 = 8$ ??

Varun Janga
  • 3
alkabary
  • 6,464
  • 6
    It’s actually the Catalan numbers that you want; sapristi has shown how to see that your numbers satisfy the same recurrence as the Catalan numbers. You may also find this question and its answers helpful. – Brian M. Scott Nov 26 '15 at 21:38
  • @alkabary A more general answer by Riordan giving the number of such chord diagrams for any number of intersections: http://www.jstor.org/stable/2005477. – Daugmented Feb 15 '18 at 02:04

2 Answers2

10

First off, there is a missing case for $n = 3$ : the one where you pair $(2,3), (1,4), (6,5)$.

Now the recursion to count the number of pairing would go like this :

Let us take a fixed point $O$ among one of the $2n$ points on the circle. A line going from this point would have to divide the circle into two regions, each containing an even number of points. There are thus $n$ possible choices for a chord leaving from $O$ (make a drawing).

Choosing one such cord will lead to unique divisions of the circle (two different cords leaving from $O$ will give different divisions). Reciprocally, any division of the circle would match with one of these cords. So we have correctly divided our problem into a set of disjoint subproblems.

Then, to get a recursive formula, we need to count how many points are on each side of the cord, for each possible cord : the regions have $(2k, 2(n-k-1))$ points, for $0\leq k \leq n-1$.

So finally, a recursive formula for $h(n)$ would be :

$h(n) = \sum_{k=0}^{n-1} h(k) \times h(n-k-1)$.

sapristi
  • 376
2

A general answer to your problem is given by free probaility in three ways:

1) Combinatoric

Catalan numbers;

2) Random matrix theory:

limiting spectral distibution of a self-adjoint gaussian random matrix or Wigner matrix;

3)Operator algebra theory:

limit of sum of independant copies of a wigner random matrix or the spectral distribution of $l(\xi)+ l(\xi)^{\ast}$ where $l(\xi)$ is a creation operator of a full Fock space $\mathcal{F}(\mathcal{H})$ on a Hilbert $\mathcal{H}\in \xi$.

Both question 2) and 3) are answered by the semi-circular law, and the event moments of the semi-circular law are the catalan numbers, which answered the first question.

Iliyo
  • 46