5

$z$ is in the complex plane, r is real, and P(z) is an nth order polynomial in z

Is there a way to determine the minimum value of $r$ for which the region $|P(z)|<r$ is a connected region? By connected I mean that any point in the region can be reached from any other point in the region by a path entirely in the region.

An equivalent question would be: Is there a way to determine at what value of $r$ the surface $P(z)=r$ changes from being a single continuous surface to multiple disconnected surfaces?

In the limit of large $r$, the region becomes one large circle. In the limit of small $r$, it becomes a set of disconnected circles, one around each root of $P(z)$.

If the threshold $r$ cannot be determined analytically for a general $P(z)$, are there non-trivial special cases of $P(z)$ for which it can?

Example:

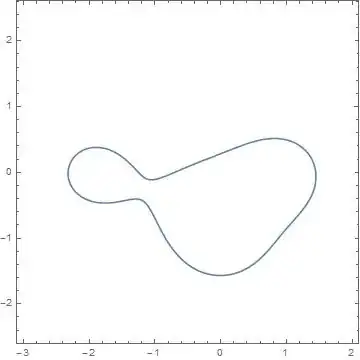
$|(z+2)(z+i)(z-1)|<2.7$

is connected.

Example0

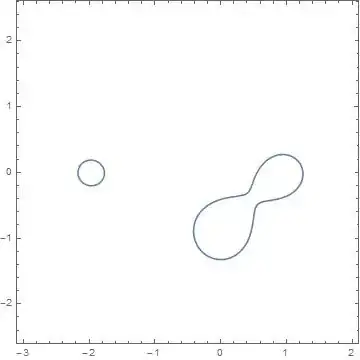
$|(z+2)(z+i)(z-1)|<1.3$

is not connected.

Example1

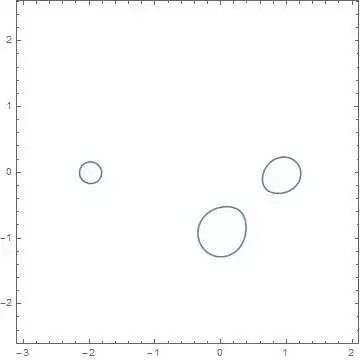
$|(z+2)(z+i)(z-1)|<1.1$

is further disconnected.

Examp;e2

Jerry Guern
  • 2,764

2 Answers2

1

A partial answer:

Notice that in this problem, when a connected region becomes disconnected, the pieces “pinch off" from one another. In other words, the enclosing surface becomes not-smooth. So if we let $P(z)=r*e^{it}$, these pinching-off points will be discontinuities in $\frac{dz}{dt}$, i.e. places where $\frac{d^{2}z}{dt^{2}}$ diverges. So we can calculate:

$\frac{dP}{dt}=\frac{dP}{dz}\frac{dz}{dt}=r*i*e^{it}$

$\frac{d^{2}P}{dt^{2}}=\frac{dP}{dz}\frac{d^{2}z}{dt^{2}}+\frac{d^{2}P}{dz^{2}}\frac{dz}{dt}\frac{dz}{dt}=-r*e^{it}$

Since all the factors in that eqn are finite, $\frac{d^{2}z}{dt^{2}}$ can only diverge where $\frac{dP}{dz}=0$.

So the pinching-off points will occur at the roots of $\frac{dP}{dz}=0$, with corresponding threshold r's equal to the value of $|P(z)|$ at those root z's.

To use the Example in the plots, $P(z)=(z-1)*(z+2)*(z+I)$

$\frac{dP}{dz}=0$ at z=(-1.15-0.27i) and z=(.486-.40i)

The corresponding respective value of r are 2.63239 and 1.26628. These pinching-off points and corresponding threshold r's are consistent with the plots.

However, using this approach require explicit calculation of the roots of $\frac{dP}{dz}=0$ which might be impractical.

Jerry Guern
  • 2,764
1

The set $\{ z:|P(z)|<r\}$ is connected if and only if $r>\max\{ |P(c)|:P'(c)=0\}$. Points $c$ such that $P'(c)=0$ are called critical points ans points $P(c)$ with these $c$ are called critical values.

To see this, consider the graph of $|P(z)|,$ or better $u(z)=\log|P(z)|$ as a mountain landscape. This landscape has no peaks (maxima) and the only pits (minima) are at the zeros of $P$. It has saddle points exactly at the critical points of $P$. Now think of the level set $\{ z:|P(z)|=r\}$ as $r$ decreases from $+\infty$. When $r$ is very large, this set consists of one big curve resembling a circle. So your set is connected (interior of this curve). When $r$ equals to the absolute value of the largest critical value, the level set must look like figure 8, and as $r$ becomes smaller it will split into two components (if the zero $P'(c)$ is simple. In general it can split into more tan 2). Each component will contain a zero of $P$ so they will never disappear, and your set will remain disconnected as $r$ decreases to $0$.

It will further split as $r$ passes other critical values until it will become a union of small discs one around each zero of $P$.

Alexandre Eremenko
  • 3,683
  • Thank you for correcting my terminology and notation. Also, your explanation in terms of saddle points was more clear than the one above about discontinuities in $\frac{d^{2}z}{dt^{2}}$. Would you have any interest in a related Question I posted? http://math.stackexchange.com/questions/1518310/how-to-prove-this-simple-polynomial-inequality – Jerry Guern Nov 08 '15 at 20:17