1

I am trying to compute this cumulate. However, with very high or very low values of x, the computation is affected by numerical errors.

$$p=1-\frac{2 u}{\sqrt{2 \pi } l \sqrt{t} e^{\frac{(l t+u x)^2}{2 t u^2}} \left(\text{erf}\left(\frac{l t+u x}{\sqrt{2} \sqrt{t} u}\right)-\text{erf}\left(\frac{l t+u (x-t u)}{\sqrt{2} \sqrt{t} u}\right)\right)+2 u}$$

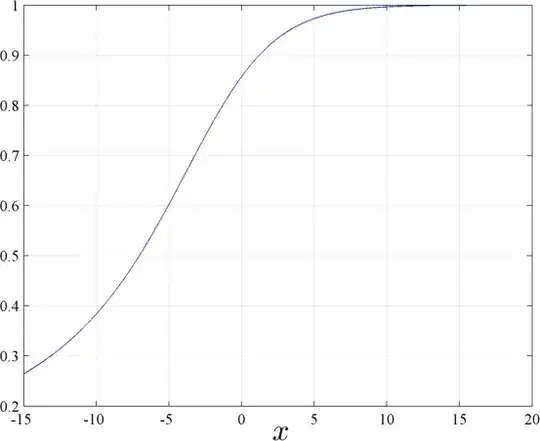
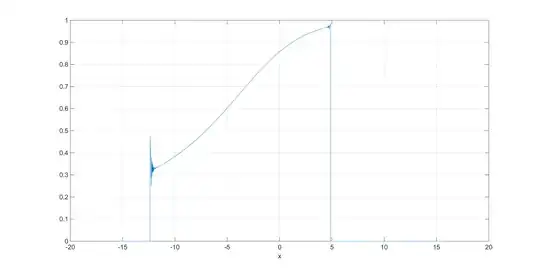
which, for t=1; u=0.5 and l=2 gives this shape which is clearly affected by numerical errors on both sides: enter image description here

I thinks the problem is due to the really high number in the exponential, which is then multiplied by the really small number of the to erf functions. I tried different solutions (mostly involving expanding the exponential) but none worked.

The computation are done in MATLAB

Any help is appreciated.

Community
  • 1
Vaaal88
  • 468

1 Answers1

1

Try writing the denominator in terms of the complementary error function $\mathrm{erfc}(x) = 1 - \mathrm{erf}(x)$. Doing so should give you more accuracy for the larger positive values of $x$. The negative values of $x$, however, are still a problem.

Here is a better solution. The function of $x$ in the denominator can be written as

$$ f(x) = \frac{2}{\sqrt{\pi}}\int_a^b \exp(-(\tau + b)(\tau - b))\,d\tau, $$

where $a = \alpha + \beta(x - tu)$, $b = \alpha + \beta x$, $\alpha = \ell t /(u\sqrt{2t})$, and $\beta = 1/\sqrt{2t}$. It follows that

$$ p = 1 - \frac{2u}{\ell\sqrt{2\pi t}f(x) + 2u} $$

For each value of $x$, use a quadrature routine with a small convergence tolerance to evaluate $f$. Doing so, you can accurately compute $p(x)$ over a wider range of values. Clearly this approach is more computationally demanding then using $\mathrm{erf}$ or $\mathrm{erfc}$, however, it should be more robust to the input value $x$. In practice, you should be able to calculate $p$ for ''not too negative'' values of $x$ using the solution mentioned above and then resort to this approach for negative values of $x$ past some cutoff. Here is a plot I made in Matlab using their $\texttt{quad}$ function to evaluate $f$ with a tolerance of $10^{-12}$, $x\in[-15,20]$, and your stated parameter values.

enter image description here

K. Miller
  • 4,808
  • Thank you for your answer. I tried it, it didn't seem to help. – Vaaal88 Sep 30 '15 at 14:09
  • It worked fine for me, the instability for the larger values of $x$ was removed. – K. Miller Sep 30 '15 at 14:27
  • The erfc solution didn't work for me, and I wonder why. I simply replaced erf with 1-erfc, but the result is exactly the same as before. The second solution works. However, it is really computationally expensive, so I wonder if there is a faster way to do this. – Vaaal88 Sep 30 '15 at 16:08
  • To be fair, the method using quadrature isn't that computationally demanding. It takes less than a minute on my laptop to compute $4000$ values of $p$ with a tolerance of $10^{-12}$. So it depends on how many values of $p$ you need and how you are using those values. – K. Miller Sep 30 '15 at 16:15
  • Yes, it's taking the same time for me. However, I am computing the value of p with many x (not more than 4000 though) and many t (around 800). I would like to be able to run everything in less than half a minute, but with this method it doesn't seem feasable. – Vaaal88 Sep 30 '15 at 16:26
  • also, with high t value the quad method become really really slow (around 25/26 s with t=10) – Vaaal88 Sep 30 '15 at 16:38
  • 1
    You could try parallelizing the runs over the different t values. – K. Miller Sep 30 '15 at 17:05
  • After playing a little bit with your solution, it seems quite fast for my purposes. Thank you. I'll wait some more to see if anybody else has a different solution, and then I'll accept it. – Vaaal88 Sep 30 '15 at 17:46
  • Let us continue this discussion in chat. – Vaaal88 Oct 01 '15 at 08:28