Numerical inverse of a function

Question

How to approximate the inverse of the function below? $$f(x) = \frac34 x - \frac 12\sin(2x) + \frac 1{16} \sin(4x)$$

The goal is to get $x$ values (range $[0, \pi]$) from values of $f$. The function doesn't seem to have analytical inverse, so I figured to approximate $f$ with a Taylor series, truncate, then try taking an inverse, eg with Mathematica's InverseSeries? http://reference.wolfram.com/language/ref/InverseSeries.html

Does anyone have a different approach, perhaps without Mathematica?

Answer 1

The problem with yours approach is that Taylor series don't approximate your function uniformly well over the whole domain $[0, \pi]$, i.e. you need different approximations on the different parts of the inverse function domain.

First, I would renorm your function to exploit symmetry $$ F(x) = \frac{f\left(\frac{\pi(x+1)}{2}\right) - f(\pi/2)}{f(\pi) - f(\pi/2)} = \frac{6 \pi x+8 \sin (\pi x)+\sin (2 \pi x)}{6 \pi } $$ This function maps $[-1, 1]$ to $[-1, 1]$ and is odd. Since it it odd, we can build inverse only for $F(x)$ mapping $[0, 1]$ to $[0, 1]$.

The function $F(x)$ is almost constant near $x = 1$. Precisely, $$ F(x) = 1+\frac{1}{30} \pi ^4 (x-1)^5-\frac{1}{252} \pi ^6 (x-1)^7+\frac{\pi ^8 (x-1)^9}{4320}+O\left((x-1)^{11}\right) $$ Truncating the series and solving a 9th degree polynomial may become a challenging problem, so let's try to match those terms with some simple invertible function, like $$ G(x) = 1 - \alpha \sin^5 (\beta \sin (\gamma(1 - x))),\\ G^{-1}(y) = 1 - \frac{1}{\gamma}\arcsin\left[\frac{1}{\beta}\arcsin\sqrt[5]{\frac{1 - y}{\alpha}}\right]. $$ Comparing the Taylor series for $F$ and $G$ around $x = 1$ one obtains a system of equations for $\alpha, \beta, \gamma$ $$ 30\alpha \beta ^5 \gamma ^5 = \pi ^4\\ 210 \alpha \beta ^7 \gamma ^7+210 \alpha\beta ^5 \gamma ^7=\pi ^6\\ 1380 \alpha \beta ^9 \gamma ^9+4200 \alpha \beta ^7 \gamma ^9+1380 \alpha \beta ^5 \gamma ^9 = \pi ^8 $$ Wolfram Mathematica seem to have no problem with solving that, resulting in two solutions ($\alpha \approx 1184.38, \beta \approx 0.2679, \gamma \approx 1.147$ and $\alpha \approx 1.6358, \beta \approx 3.732, \gamma \approx 0.3073$), I suggest using the second $$ \alpha = \frac{784 \sqrt{7}}{15 \left(2+\sqrt{3}\right)^{5/2} \pi }, \quad \beta = 2+\sqrt{3}, \quad \gamma = \frac{\pi }{2 \sqrt{7 \left(2+\sqrt{3}\right)}} $$ 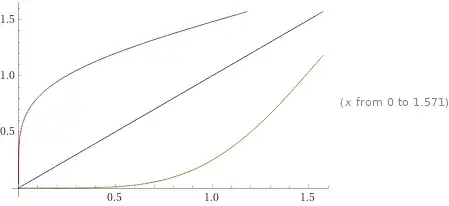The graphs look very close, but that might be misleading, since $F'(x) \approx 0$ when $x > 1/2$.

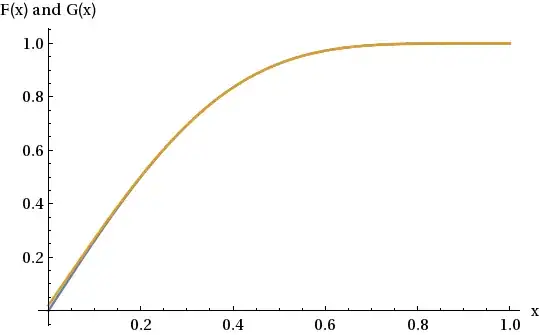
This approximation gives a $|G^{-1}(y) - F^{-1}(y)| < 0.000697727 < 10^{-3}$ solution when $y \in [0.5, 1]$

Let's perform similar approximation for $y \in [0, 0.5]$. $$ H(x) = \alpha \sin(\beta \sin (\gamma x))\\ H^{-1}(y) = \frac{1}{\gamma} \arcsin \left[\frac{1}{\beta} \arcsin \frac{y}{\alpha}\right] $$ Comparing Taylor series up to $O(x^7)$ gives a system of equations for $\alpha, \beta, \gamma$ $$ \alpha = \frac{16}{3\pi}, \quad \beta = \frac{1}{\sqrt{3}}, \quad \gamma = \frac{\sqrt{3}\pi}{2}. $$

This approximation to $F^{-1}(y)$ achieves accuracy of $0.0000176652$ when applied on $y \in [0, 0.5]$.

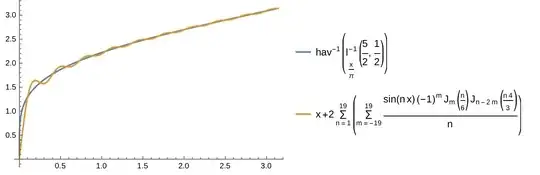
Here's the log-plot of the absolute error given by two approximations (blue - $10^{-3}$, orange - $|F^{-1}(y) - G^{-1}(y)|$ and green - $|F^{-1}(y) - H^{-1}(y)|$)

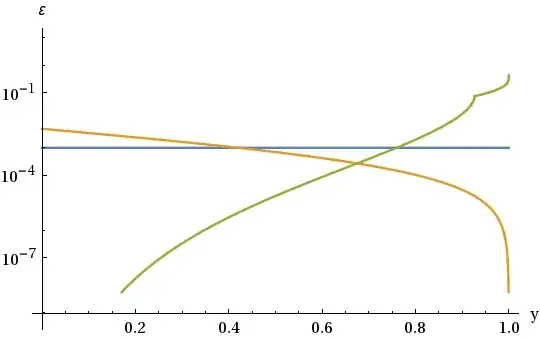
It follows that $H^{-1}(y)$ can be used on $[0, 0.6296]$ and $G^{-1}(y)$ on $[0.6296, 1]$ with absolute error not exceeding $\epsilon = 1.36 \cdot 10^{-4}$.

To refine the result in the middle you can use one-two Newton iterations $$ x_{n+1} = x_n - \frac{F(x_n)-y}{F'(x_n)} = x_n - \frac{6\pi x_n+8\sin \pi x_n + \sin 2\pi x_n - y}{16\pi\cos^4 \frac{\pi x_n}{2}} $$

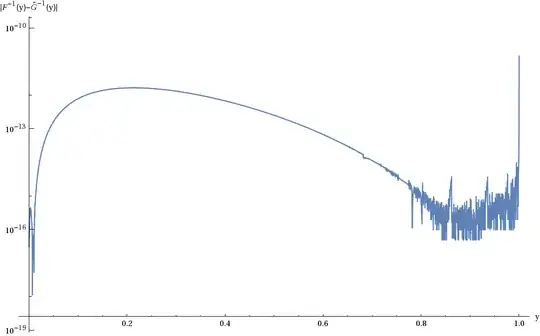
Here's a plot of $|F^{-1}(y) - \tilde G^{-1}(y)|$ where $\tilde G^{-1}(y)$ is computed as $G^{-1}(y)$ with two Newton iterations. The overall accuracy is better than $10^{-10}$:

Answer 2

You could try a root-finding method. If you have that $c$ is an $f$-value, then you can solve $h(x) = f(x) -c =0$ on $[0,\pi]$ via Newton's method or the secant method, for example.

Answer 3

Special Function Solution:

Ironically, you can get a closed, quantile special function, inverse using this special case of Incomplete Beta function with Mathematica’s Inverse Beta Regularized, but parameters beyond $\frac52$ produce very specific equations:

$$\text B_{\sin^2(x)}\left(\frac52,\frac12\right)=\frac{3x}4-\frac12\sin(2x)+\frac1{16}\sin(4x)\implies \boxed{x\mathop=^{0\le x\le\frac{3\pi}8}_\text{one period}\sin^{-1}\sqrt{\text I^{-1}_\frac{8x}{3\pi}\left(\frac52,\frac12\right)}}$$

Use the periodicity of the original function to extend the domain of the inverse function:

Proof of result. Please correct me and give me feedback!

The error of the Taylor series to $n$ terms is given by:

$$\text B_{\sin^2(x)}\left(n+\frac52,\frac12\right)$$

Therefore, the inverse of the error of the Taylor series of $$\frac{3x}4-\frac12\sin(2x)+\frac1{16}\sin(4x)$$ to $n$ terms experimentally on $0\le x\le\frac{3\pi}8$ is:

$$\sin^{-1}\sqrt{\text I^{-1}_\frac{8x}{3\pi}\left(n+\frac52,\frac12\right)} $$

$\DeclareMathOperator\Re {Re}$Fourier Series Solution:

We invert a simpler form of $f(x)$: $$f(x) = \frac34 x - \frac 12\sin(2x) + \frac 1{16} \sin(4x)\implies g(x)=\frac83f\left(\frac x2\right)=x-\frac43\sin(x)+\frac16\sin(2x)$$

which has points at $(\pm\pi,\pm\pi)$, so we apply the complex Fourier series to $h(x)=g^{-1}(x)$, substitute $t\to g(t)$ and integrate by parts:

$$h(x)=\sum_{n\in\Bbb Z}e^{inx}\frac1{2\pi}\int_{-\pi}^\pi h(t)e^{-i nt}dt=\Re\sum_{n=1}^\infty e^{inx}\frac1\pi\int_{-\pi}^\pi te^{-i n g(t)}dg(t)= \Re\sum_{n=1}^\infty e^{inx}\left(\frac{2i}n(-1)^n-\frac i{\pi n}\int_{-\pi}^\pi e^{-i n g(t)}dt\right)$$

Next, use logarithm’s Taylor series to get a $\Re(i\ln(z))=-\operatorname{Im}(\ln(z))$ expression and apply the Jacobi Anger expansion

$$h(x)=x-\Re\sum_{n=1}^\infty ia_n\frac{e^{i nx}}n,a_n=\frac1\pi\int_{-\pi}^\pi e^{i n\left(-t+\frac43\sin(t)-\frac16\sin(2t)\right)}dt=\frac2\pi\sum_{m\in\Bbb Z}J_m\left(-\frac n6\right)\int_0^\pi\cos\left((2m-n)t+\frac43\sin(t)\right)dt$$

Now the Bessel J integral representation and $J_n(x)$’ properties are used. Additionally, the inverse haversine appears. Therefore:

$$g(x)=x-\frac43\sin(x)+\frac16\sin(2x)\implies g^{-1}(x)\mathop=^{0\le x\le\pi}\operatorname{hav}^{-1}\left(\text I^{-1}_\frac x\pi\left(\frac52,\frac12\right)\right)=x+2\sum_{n=1}^\infty\sum_{m\in\Bbb Z}\frac{(-1)^m\sin(nx)}mJ_m\left(\frac n6\right)J_{n-2m}\left(\frac{4n}3\right)$$

where the sum is a global inverse. Also, if $m$ is summed over, one gets a “two variable Bessel function”, but it is not a standard function. Replacing $\frac43$ and $\frac16$ with other number likely would expand other inverses as a series. The series is shown here: