7

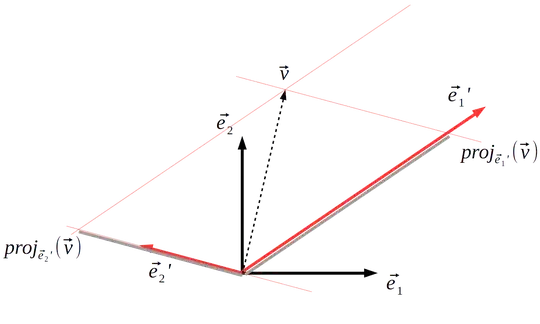
I have a vector, originally expressed in the standard coordinates system, and want to perform a change of basis and find coordinates in another basis, this basis being non-orthogonal.

  • Let $B = \{e_1, e_2\}$ be the standard basis for $\Bbb R^2$.
  • Let $B' = \{e_1', e_2'\}$ be a non-orthogonal basis for $\Bbb R^2$.
  • Let $v$ be some vector in $\Bbb R^2$.

The standard inner product is

$\langle a, b \rangle = \sum_{i=0}^n a_i b_i.$

I want to define an inner product in the non-orthogonal basis $B'$ so that $\langle e_1', e_2' \rangle_{B'} = 0$ since $\sum_{i=0}^n e_{1i}' e_{2i}' \neq 0$.

Basically, I want to use this new inner product to get the component/coordinates of the vector $v$ on the basis $B'$.

enter image description here

Mateen Ulhaq
  • 1,281
joseph M'Bimbi-Bene
  • 251
  • 1
    By the way, $\langle, \rangle$ may be achieved with \langle, \rangle. They play more nicely with the TeX layouts than < and > . – Patrick Stevens Aug 25 '15 at 07:32
  • What you want seems confused to me. You do not need any inner product to perform a change of basis, and you certainly shouldn't be using two different inner products unless you have a very specific reason to do so. – Marc van Leeuwen Aug 25 '15 at 07:45

3 Answers3

4

What you want to do is change the basis of the vectors you are working with, then take the inner product on that. since $e_1', e_2'$ are a basis for $\mathbb{R}^2$, every vector $v$ = $v_1 e_1' + v_2 e_2'$ for unique values $v_1, v_2$. Then you set $\langle v, w \rangle = v_1 w_1 + v_2 w_2$

To find an explicit method of converting a vector into this new coordinate system, look into change-of-basis matrices. if $e_1' = a_1 e_1 + a_2 e_2, e_2' = b_1 e_1 + b_2 e_2$, take the matrix with $$ \left( \begin{array}{cc} a_1 & b_1 \\ a_2 & b_2 \end{array} \right) $$ and take its inverse. Then if $\langle v, w \rangle'$ is your new inner product, you have $\langle v, w \rangle'= \langle M^{-1}v, M^{-1}w \rangle$.

Marc van Leeuwen
  • 119,547
user264059
  • 148
0

Let u,v be any lin ind vectors in the plane. Define u.u=a>0,u.v=0=v.u,v.v=b>0. Extend this linearly for all pairs of vectors. It is easily verified that this is an inner product.

Adelafif
  • 1,343
0

If you write down a $2\times 2$ matrix $P$ whose columns are formed by the coordinates of $e'_1,e'_2$ in the standard basis, then multiplication (on the left) by $P$ does the following in terms of coordinates. If $x,y\in\Bbb R$ these can be interpreted as coordinates of a vector $v$ with respect to the new basis $e'_1,e'_2$, in other words one takes $v=xe'_1+ye'_2$; then $\binom rs=P\binom xy$ gives the coordinates of$~v$ in the standard basis $e_1,e_2$, that is, $v=re_1+se_2$. To see why this is true, note that by definition of$~P$ it is true when $(x,y)=(1,0)$ and also when $(x,y)=(0,1)$ (one gets $v=e'_1$ respectively $v=e'_2$); the general case now follwos by taking linear combinations of these special cases.

But what you want is the opposite: you want to find the coordinates in the new basis of a vector given by its coordinates $\binom rs$ in the standard basis. Therefore you need to compute the inverse matrix $P^{-1}$, and the desired coordinate change is given by (left) mluitplication by$~P^{-1}$.

Note that no inner product plays a role in any way when doing change of basis.

Marc van Leeuwen
  • 119,547
  • obtaining the components on ${e_1, e_2}$ was just an illustration, i really wanted to define an inner product on this basis.

    And thank you, your first answer gave me the solution

     – joseph M'Bimbi-Bene Aug 25 '15 at 11:32