An equality for the dimension of the sum of subspaces (in the non-degenerate case)

Question

This post is a sequel of An inequality for the dimension of the sum of subspaces, inspired by this famous answer on $\dim(U+V+W)$.

The inequality $$\dim(\sum_{i = 1}^{n} U_i) \le \sum_{r=1}^{n} (-1)^{r+1} \sum_{i_1 < i_2 < \dots < i_r} \dim(\bigcap_{s=1}^{r}U_{i_s}) $$

is an equality for $n \le 2$, is true for $n = 3$ (but not an equality in general, see here), and false for $n \ge 4$ (see the answers of Quid and Darij Grinberg in the first link).

The set of intersections of the form $\bigcap_{s=1}^{r}U_{i_s}$ with $0 \le r \le n$ and $i_1 < i_2 < \dots < i_r$ is a finite poset.
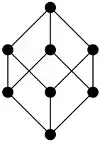
The system is called non-degenerate if the $2^n$ intersections above are $2$-$2$ distinct, which implies that the poset above is a boolean (algebra) lattice $B_n$; for example $B_3$ is :

The counter-examples for the equality at $n=3$ and for the inequality at $n=4$, are both degenerate.

Question: Is the equality (or at least the inequality) true in the non-degenerate case?

Take my counterexample $\left(U_1, U_2, U_3, U_4\right)$, and take a non-degenerate quadruple $\left(V_1, V_2, V_3, V_4\right)$ for which equality holds (e.g., pick a $4$-dimensional vector space with basis $e_1,e_2,e_3,e_4$, and let $V_i$ be the span of $e_1,e_2,\ldots,\widehat{e_i},\ldots,e_4$). Now $\left(U_1\oplus V_1,U_2\oplus V_2,U_3\oplus V_3,U_4\oplus V_4\right)$ (in the direct sum of the ambient spaces of the two quadruples) should be a non-degenerate counterexample. — darij grinberg, Jul 28 '15 at 12:40
Thanks. So, what does it mean for a bunch of things to be "2 by 2 non-equal"? Is it different from just saying the things are distinct? — Gerry Myerson, Jul 28 '15 at 12:56
@darijgrinberg: you're right! What if we add the assumption "irreducible" (i.e. not the direct sum of two systems)? — Sebastien Palcoux, Jul 28 '15 at 13:07
Hmm. I fear this is becoming more and more a question about indecomposable representations of the four-subspaces quiver... — darij grinberg, Jul 28 '15 at 13:15
It isn't (e.g., https://daim.idi.ntnu.no/masteroppgave?id=4316 ), but the characterization is beyond my understanding. — darij grinberg, Jul 28 '15 at 13:26

score 1 · Accepted Answer · edited Apr 13 '17 at 12:21

1

It is still false.

Take my counterexample $\left(U_1,U_2,U_3,U_4\right)$ from An inequality for the dimension of the sum of subspaces , and take a non-degenerate quadruple $\left(V_1,V_2,V_3,V_4\right)$ for which equality holds (e.g., pick a $4$-dimensional vector space with basis $e_1,e_2,e_3,e_4$, and let $V_i$ be the span of $e_1,e_2,\ldots,\widehat{e_i},\ldots,e_4$). Now $\left(U_1\oplus V_1,U_2\oplus V_2,U_3\oplus V_3,U_4\oplus V_4\right)$ (in the direct sum of the ambient spaces of the two quadruples) should be a non-degenerate counterexample.

edited Apr 13 '17 at 12:21

Community

1

answered Jul 30 '15 at 14:10

darij grinberg

19,173

Nice thank you! I've open a new post on MO for a non-degenerate indecomposable system, in the more general case of a finite factor, see here. In the von Neumann algebra theory, a matrix algebra $M_{n}(\mathbb{C})$ is a finite factor of type ${\rm I}_n$, but there also exists finite factors of type ${\rm II}_1$, for which the problem makes sense. – Sebastien Palcoux Jul 30 '15 at 14:34

An equality for the dimension of the sum of subspaces (in the non-degenerate case)

1 Answers1