My friend and I decided to meet between 1 and 3 PM today. There is a condition that whoever arrives first will not wait for the other for more than 20 minutes. what is the probability that we'll meet today?
Asked
Active
Viewed 771 times
0
-
Probably not your fault because questions like this are often given as homework, but it really is an annoying question. Are you supposed to assume that the arrival times of you and your friend are uniformly distributed between 1 and 3 PM? – Stanley Jun 27 '15 at 04:29
-
yes,arrival times are uniformly distributed. – Katherine Jun 27 '15 at 04:45
-
To help you get started, read this answer, which deals with a slightly different problem. You just have to think of the two arrival times as points on an interval. – JimmyK4542 Jun 27 '15 at 05:03
-
Look at the Related column on the right. – Jun 27 '15 at 05:03
1 Answers
3
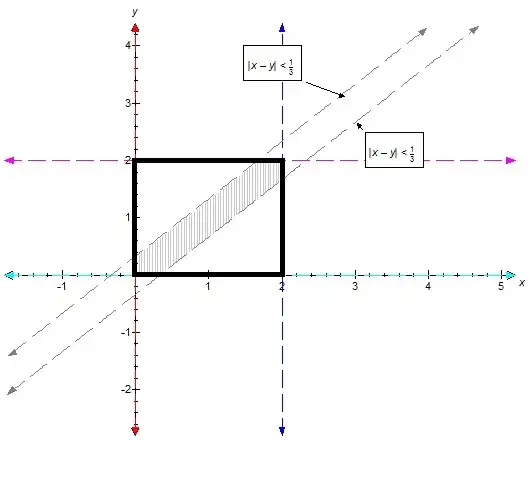 $$20 min=\frac{1}{3}$$ hour
$$20 min=\frac{1}{3}$$ hour
meeting condition equal to $|x-y|<\frac{1}{3} $
$$S=\{(x,y)| 0\leq x\leq 2 ,0\leq y\leq 2\}$$ that means 1 to 3 pm ,for each person 2 hour is possible
$$ p(|x-y|<\frac{1}{3})=\frac{shaded \space area }{2*2}$$
N. F. Taussig
- 79,074
Khosrotash
- 25,772