I want to find the maximum possible area of a right triangle with hypotenuse $=10$. My approach so far: let $x,y$ be the lengths of the two sides adjacent to the right angle; then $$100=x^2+y^2$$
Area $=\frac{xy}{2}$, so by the substitution method I got equality. But my result is wrong (probably I made a mistake in the equality), could someone show what to do?
There are already some good answers, but as the question is tagged geometry, I wanted to post a bit less algebraic solution (see also this question).
Hint:
$\hspace{70pt}$
I hope this helps $\ddot\smile$
$$(x-y)^2=x^2+y^2-2xy=100-2xy\ge 0\iff \frac{xy}{2}\le 25$$
with equality iff $x=y>0$, i.e. $2x^2=100\iff x=y=\sqrt{50}=5\sqrt{2}$.
As you said, we have $100 = x^2+y^2$ so that $y= \sqrt{100-x^2}$ and thus the area is $$A= \frac{xy}{2}=\frac{1}{2}x\sqrt{100-x^2}.$$ Now, let $f(x)= \frac{1}{2}x\sqrt{100-x^2}$ and maximize this function over $x\geq 0$, e.g. by looking when $f'(x)=0$ to find its critical points.
Let the non-hypotenuse sides of the triangle be $(a,b)$. Then the hypotenuse is $\sqrt{a^2+b^2}$ and the area is $A = \frac{ab}{2}$. So
$$a^2+b^2 = 100\\ A^2 = \frac14 a^2b^2 = \frac14 a^2 (100-a^2) \\ $$
Maximizing $A^2$ maximizes $A$, and $$ \frac{d(A^2)}{da} =\frac14( 200a -4a^3) $$ which is zero at $a = \sqrt{50}$ making $b=\sqrt{50}$ as well and the area $A = \frac12\sqrt{50}^2 = 25$
Let's use Lagrange Multipliers as this is a Maxima-Minima problem. We have the constraint $x^2+y^2=100$ and the function to maximize is ${{x \cdot y} \over 2}$
Taking the gradients, derivatives with respect to both variables, and equating we get a system of equations.
$$2x=\lambda \cdot {y \over 2}$$ $$2y=\lambda \cdot {x \over 2}$$
Which simplifies to
$$4 \cdot x= \lambda \cdot y$$ $$4 \cdot y= \lambda \cdot x$$
The equations are symmetric so we know that $x=y$
Substituting this into the constraint $x^2+y^2=100$, we get
$$2x^2=100 \Rightarrow x=5 \cdot \sqrt2$$ and $$2y^2=100 \Rightarrow y= 5 \cdot \sqrt2$$
So the maximum area is ${25}$
A little geometry:
Draw a line and a circle with radius $5$, and center on the line.
Call the points of intersection of circle and line $A$ and $B$.
This circle is the $Thales$ circle, diameter AB. Take any point on the circle, call it $C$.
All vertices,$\, C$, of right triangles with hypotenuse 10 are on this circle.
Area of a triangle: $ Area$ = $1/2 × base × height$.
1) $Base = 10$, given.
2)$ Maximal \, height $ of triangles with vertices on the circle is clearly the
$ radius = 5$;
($ABC$ is isosceles in this case).
$Maximal \, area = 1/2 × base × height = 1/2 × 10 × 5 = 25$.
Comments welcome!
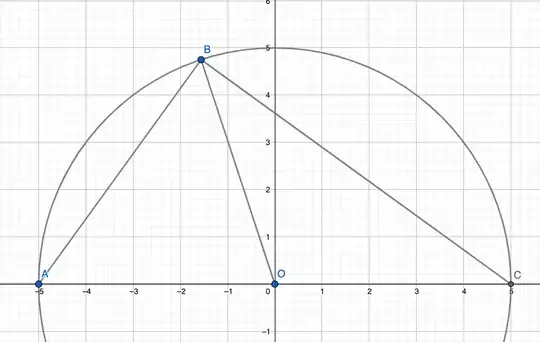
The area of triangle $ABC$ is just $\Delta ABO + \Delta BOC$. If $\angle BOC = \theta$, the area is:
$$\frac{1}{2} r^2 \sin \theta + \frac{1}{2}r^2 \sin(180 - \theta) = \frac{1}{2}r^2 \big( \sin \theta + \sin(180 - \theta) \big) = \frac{1}{2}r^2 (2 \sin \theta) = r^2 \sin \theta$$
where we have used the identity $\sin \theta = \sin(180 - \theta)$.
The maximum value of $\sin \theta$ is $1$, so the maximum area is $r^2$. In this case, $r = 5$ so the maximum area is $25$.
This occurs when $\theta = \frac{\pi}{2}$ or $90º$, so $\Delta ABC$ must in fact be isoceles.
Alternatively, if $A = (-5,0)$, $B = (5 \cos t, 5 \sin t)$, $C = (5,0)$, then the area of $\Delta ABC$ using the shoelace formula is:
$$ \begin{vmatrix} 5 & 0 \\ 5 \cos t & 5 \sin t \\ -5 & 0 \\ 5 & 0 \\ \end{vmatrix} $$
so the area is: $$\frac{1}{2} \big((25 \sin t + 0 + 0) - (0 + -25 \sin t + 0) \big) = 25 \sin t$$
which takes the maximum value $25(1)$ when $t = \frac{\pi}{2}$, again.
The area of triangle $ABC$ is can also be computed using determinants:
$$ \begin{vmatrix} 5 & 0 & 1 \\ 5 \cos t & 5 \sin t & 1 \\ -5 & 0 & 1 \\ \end{vmatrix} $$
which when computed, gives:
$$\frac{1}{2} \left((25 \sin t + 0 + 0) - (-25 \sin t + 0 + 0) \right) = 25 \sin t.$$
