Why is $\sum_{n=0}^{\infty }\left ( \frac{1}{2} \right )^{n}= 2$?

Question

I'm sorry if this is duplicated, but I can not find any answer to it.

Answer 1

the geometric series for $|x|<1$ $$1+x+x^2+x^3+....=\frac{1}{1-x}$$ use $x=0.5$ $$1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...=\frac{1}{1-\frac{1}{2}}=2$$

Answer 2

Here is a nice proof without words:

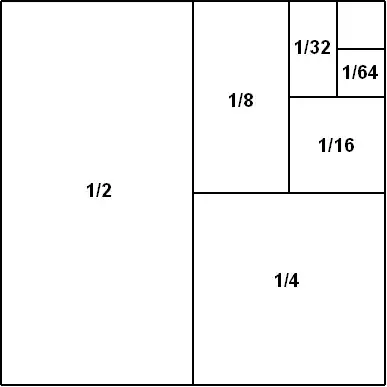
Obviously, this doesn't replace an airtight proof, but it is great for intuition.

Answer 3

An explanation for the geometric series: $(1-x)(1+x+x^2+...+x^n) = 1-x + x-x^2 +x^2 - x^3 + ... + x^n - x^{n+1} = 1-x^{n+1}$ for $n \to \infty$ and $x=\frac 1 2$ you get your series, since $(\frac 1 2)^n \to 0$.