I'm currently studying operations research and I want to know and understand how we find an optial solution to the dual problem with minimum effort. Lets say we have this primal and dual problem:
The canonical view of the primal problem:
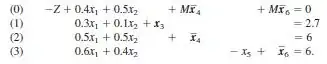
And the solution to the primal problem:
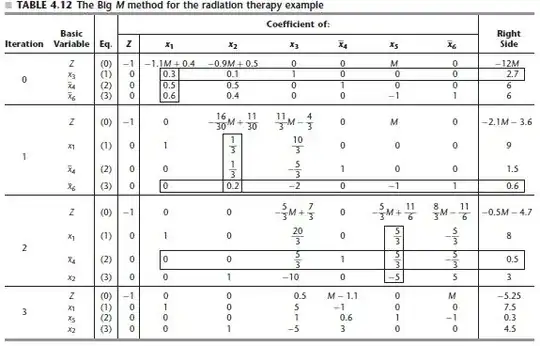
I was told that there was an easy way of finding an optimal solution for dual problem (one that does not apply the simplex method to the dual problem because we have solved the primal) by using the last tableau of the primal problem.
I'm really lost here and there was no info in my textbook on this. So please some help on this will be great.
Ok I found some info on this on a presentation.
First they had these primal and dual problems:
Then they did the canonical form of the primal problem and dual problem(for the dual I have some dificulty with the last 2 equations, need some explainig why they are exactly that):// Never mind I figured it out
And finaly for the optimal solution to the dual problem it said to use :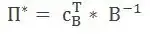
Where $c_{B}^{T}$ is the transposed vector of the coeficients of the basic variables in the last tableau , but which exactly coeficient I didn't understand( It's not written in english). I think it's those written in objective function before the first iteration. Also for $B^{-1}$ it said it consisted of the vector columns of the first basic variables ( those used in the begging) in the last tableaux.
So for example in the first problem it would give $$(0.4 , 0 , 0.5) * \begin{pmatrix} 5 & -1 & 0 \\ 1 & 0.6 & -1 \\ -5 & 3 & 0 \end{pmatrix} $$
Where $c_{B}^{T} = (x1,x5,x2)$ taken from the objective function before the first iteration and $B_{-1} = (x3,x4,x6) $ where the variables represent their columns in the last tableaux.
So what do you think guys. Is this method correct? Also can you explain to me the logic of how to achive the cannonical form of the dual problem in the 5th picture from the top down. Thanks in advance :)
