Number of ways to connect sets of $k$ dots in a perfect $n$-gon

Question

Let $Q(n,k)$ be the number of ways in which we can connect sets of $k$ vertices in a given perfect $n$-gon such that no two lines intersect at the interior of the $n$-gon and no vertex remains isolated.

Intersection of the lines outside the $n$-gon is acceptable. Obviously, $k|n$, and $n$ can't be prime because otherwise there will be dots left unconnected. The $n$-gon itself is an acceptable solution to a connection of $n$ vertices, and in the case of $k>2$, these aren't lines, but a set of connected lines, a sort of a network formed by connected planar graphs with straight edges with $k$ vertices, which are required to be vertices of the $n$-gon itself.

There must always be $S =\frac nk$ sets of lines. For $k=2$, there are exactly $\frac nk$ lines, and for $k>2$, there are exactly $\frac nk$, not lines but sets of such connected planar graphs.

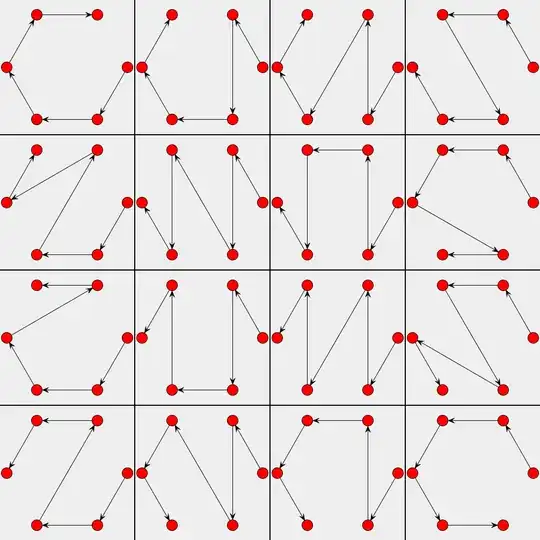
Take for example $Q(6,2)$. We have a perfect hexagon. By brute-forcing with pencil and paper, I found that there are 5 ways to connect sets of 2 vertices (dots) such that no two lines intersect inside the hexagon. Hence, $Q(6,2) = 5$.

The following image depicts the case of $Q(6,2)$:

I know for sure that an elegant solution exists for $k=2$, but I can't figure it out. For generality I ask about any amount of $k$ dots.

It's also extremely important to note we're not dividing the $n$-gon into $k$-gons, but connecting paths between $k$ nodes/vertices/dots.

Now let's move one step further:

Let $U(n,k)$ be the number of unique ways to connect sets of $k$ dots in a perfect $n$-gon, such that no two lines intersect, and rotational symmetry is neglected, i.e, every possible arrangement is unique and can't be formed by rotating or flipping another arrangement in any way. $U(6,2)=2$. Note that $U(6,2)=2$ because the arrangements of the first line in the image are not unique, and can be formed by rotating one another. The same happens for the second line of arrangements. This results in only 1 unique arrangement for each line. Hence $U(6,2)=2$.

I'm pretty clueless about both functions $U$ and $Q$, and I couldn't derive an algorithm or formula to any of them. Hence I'm posting this here.

I'm pretty sure there's a pure combinatorial approach to this problem, perhaps involving Polya's Enumeration Theorem (PET). Is there an elegant solution to these functions? Can they even be solved for $k>2$?

Any light shed on any of the functions will be very much appreciable, as I haven't been successful in deriving a formula for any of them.

EDIT - Temporary Solutions + Relevant questions AND progress

$$Q(n,2) = C_{n \over 2}\quad\text{where}\quad C_n = \frac{1}{n+1} {2n\choose n}$$ And $C_n$ denotes the $n$'th Catalan number.

Now let us denote $W(n) = U(n,2)$. Can you find a formula for $W(n)$? Perhaps a connection between $Q(n,2)$ and $W(n)$?

Another EDIT: (2)

$$Q(k,k) = k\cdot 2^{k-3}$$

EDIT 3

It seems like in general, $Q(n,3)$ is given here: https://oeis.org/search?q=3%2C27%2C324&sort=&language=english&go=Search

Perhaps generalization to higher powers will result in the general $Q(n,k)$ function..

EDIT 4

Here is a small table of values for $Q(n,k)$, which seems to be correct, provided by fabian's algorithm: (Table is in the form $Q(x\cdot k,k)$)

$$ \begin{array}{c|rrrrr} {_k\,\backslash\, ^n} & k & 2k & 3k & 4k & 5k \\ \hline 2 & 1 & 2 & 5 & 14 & 42\\ 3 & 3 & 27 & 324 & 4455 & 66339\\ 4 & 8 & 256 & 11264 & 573440 & 31752192\\ 5 & 20 & 2000 & 280000 & 45600000 & 8096000000\\ 6 & 48 & 13824 & 5640192 & 2686058496 & 1396580548608\\ \end{array} $$

EDIT 5 - $Q(n,k)$ SOLVED

As beautifully found and explained by @CuddlyCuttlefish in his answer, the formula for $Q(n,k)$ is as follows: $$Q(n,k) = \frac{(n)_{\frac{n}{k}-1}}{\left(\frac{n}{k}\right)!}\cdot (k\cdot 2^{k-3})^{\frac{n}{k}} \quad\text{where}\quad (n)_j = n(n-1)...(n-(j-1))$$

And $(n)_j$ is the falling factorial, defined as above.

Now moving to $U(n,k)$

Now it only remains to find a formula or an algorithm for $U(n,k)$. Personally I think it has to do with Polya's Enumeration Theorem and Burnside's lemma, combined with the cycle-index of the symmetric group, $Z(S_n)$. I've touched upon something related to that, and thus I think it's related. I'm not 100% sure but my instincts tell me it's related.

EDIT 6

In order to make it clear, I'm hereby adding a picture to describe the case of $U(6,3)$ and by that to clarify better what $U(n,k)$ means.

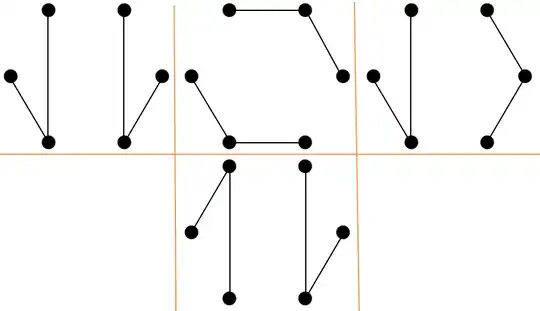
$U(6,3)=4$, as shown in the picture above (@Marko Riedel has pointed out an additional arrangement which I had previously missed). There are four unique arrangements to connect sets of 3 vertices such that no vertice remains isolated, no lines intersect at the interior of the hexagon, and each arrangement is unique and can't be formed by rotating or flipping any other arrangement.

There are two unique path-types, one that is introduced by connecting 3 adjacent vertices ($p_1$), and another that connects 2 vertices with a little "jump", and the third vertice is then adjacent ($p_2$).

Hope it makes things a bit clearer..

EDIT 7

As provided by @Marko Riedel's algorithm, $U(n,3)$ sequence starts as follows:

$$1, 4, 22, 201, 2244, 29096, 404064, 5915838,\ldots$$

Computation was very rough, and calculation times were long. That's about as efficient as it gets, as of now. Producing more values just consumes either too much memory, time or both. Refer to Marko Riedel's answers for more sequences and further explanations. Also if anybody can verify the above it would be great.

Answer 1

We can count the number of partitions described above by first dividing the $n$-gon into non-intersecting $k$-gons, then creating the $k$-paths within the $k$-gons.

The number of decompositions of an $n$-gon into $\frac{n}{k}$ non-intersecting partitions of size $k$ is $$Q'(n,k) = \frac{(n)_{\frac{n}{k}-1}}{\left(\frac{n}{k}\right)!}$$ Where $(n)_j$ is the falling factorial. This is a specific case of a result of Kreweras (in translation).

Now, within each $k$-gon, we can start at any of $k$-vertices (k choices) and create a non-intersecting path by proceeding clockwise or counter-clockwise to the nearest vertex in the $k$-gon (2 choices) with the last vertex forced. This will count each path twice, as a valid path can begin from either of its two ends. This yields

$$\frac{k2^{k-2}}{2} = k2^{k-3}$$

Ways to create a valid path inside the $k$-gon (see @fabian's answer for the original explanation).

Then for each $n$-gon, we have $\frac{n}{k}$ distinct $k$-gons with which to make the paths, giving

$$(k2^{k-3})^{\frac{n}{k}}$$

valid path configurations for each $k$-gon configuration. Combining the two results gives

$$Q(n,k) = (k2^{k-3})^{\frac{n}{k}} \times Q'(n,k) = (k2^{k-3})^{\frac{n}{k}}\frac{(n)_{\frac{n}{k}-1}}{\left(\frac{n}{k}\right)!}$$

Answer 2

You can do the calculation on the recursive formula for that problem.

You can observe the following:

• we don't need to restrict ourselfs to regular polygons, the numbers remain the same, if strictly convex polygons are used.

• there are $k \cdot 2^{k-3}$ ways to combine $k$ nodes to paths such that no line on the path crosses another line of the path (choose the starting point ($k$ possibilities), then you can choose $k-2$ times, if the next node is the next node not already on the path clockwise or counterclockwise from the start node; That makes $k \cdot 2^{k-2}$ paths, but every path was counted exactly twice)

  Example with 6 nodes:

  All those paths start at the rightmost node. We start with all choosing all nodes to be the next node counterclockwise from the start node (0000), then "count up" to choosing all nodes to be the next node counter-clockwise from the start node (1111); (0001 means choosing the first node to be the next node counter-clockwise from the start node and all the rest to be the next node clockwise from the start node)

  

  Note that all those paths are different, but if we use all nodes as starting nodes, then the path using the end node as start node and the start node as end node and connecting the same nodes cannot be distinguished in the end, since paths are not directed. E.g. the first path would be the same as the last path with start and end point exchanged.

• The number of nodes that can be "skipped" between nodes on one path can only be a multiple of $k$

• Graphs can be recursively constructed like this: choose $k$ nodes, such that there are only multipes of $k$ between 2 neighboring nodes, if enumerated clockwise (whole polygon). Choose any way to connect those nodes to a path $p$ such that the lines don't intersect. For each of the $k$ (possibly empty) sets of nodes between nodes on $p$ if enumerated clockwise(whole polygon) recursively construct the paths.

• The recursive definition of $Q$ is:

  $Q(n, k) = k \cdot 2^{k-3} \cdot\sum\limits_{\substack{p_1, p_2, ..., p_{k-1} \in \mathbb{N}\\p_1 + p_2 + ... + p_{k-1} \leq n/k-1}} Q(k \cdot(n/k-1-\sum\limits_{j=1}^{k-1} p_i), k) \cdot \prod\limits_{i=1}^{k-1} Q(p_i \cdot k, k)$

  $Q(0, k) = 1$

This is a dynamic programming approach to calculate $Q(n, k)$ (called like this: new PolygonLinesCombinations(k).getResult(n))

import java.math.BigInteger;
import java.util.ArrayList;
import java.util.Arrays;

public class PolygonLinesCombinations {

    public static void main(String[] args) {
        System.out.println(new PolygonLinesCombinations(Integer.parseInt(args[1]))
                .getResult(Integer.parseInt(args[0])));
    }

    public PolygonLinesCombinations(int k) {
        if (k < 2) {
            throw new IllegalArgumentException("k >= 2 expected, but found " + k);
        }
        this.k = k;
        this.results = new ArrayList<>();
        this.kDec = k - 1;
        this.factor = planarLineNumber(k);
        this.partition = new int[kDec];

        // exactly 1 way to connect 0 nodes
        this.results.add(BigInteger.ONE);

        // exactly 1 way to choose the rest
        this.results.add(this.factor);
    }

    private final int k;
    private final BigInteger factor;
    private final int kDec;
    private final ArrayList<BigInteger> results;
    private final int[] partition;

    public BigInteger getResult(int n) {
        if ((n % this.k) != 0) {
            throw new IllegalArgumentException("n is not divisible by k; n=" + n + ";k=" + k);
        }

        // calculate all missing results with increasing n
        int m = n / k;
        for (int i = results.size(); i <= m; i++) {
            results.add(calculateResult(i));
        }
        return results.get(m);
    }

    private BigInteger calculateResult(int m) {
        // nodes remaining, after this set is chosen
        int remainingPartitions = m - 1;
        Arrays.fill(partition, 0);

        BigInteger possibilities = BigInteger.ZERO;

        int sum = 0;
        do {
            // number of possiblities for this partition
            // = product of the number of possibilities for each remaining part
            BigInteger possibilitiesForPartition = this.factor;
            for (int i = 0; i < kDec; i++) {
                possibilitiesForPartition = possibilitiesForPartition.multiply(results.get(partition[i]));
            }
            possibilities = possibilities.add(
                    possibilitiesForPartition.multiply(results.get(remainingPartitions - sum)));

            // generate next ordered partition
            for (int i = 0; i < kDec; i++) {
                partition[i]++;
                sum++;
                if (sum > remainingPartitions) {
                    // reset to 0, if a partition gets too large
                    sum -= partition[i];
                    partition[i] = 0;
                } else {
                    break;
                }
            }
        } while (sum > 0); // stop, if all-zeroes partition is reached again

        return possibilities;
    }

    // returns n * 2^(n-3)
    private static BigInteger planarLineNumber(int k) {
        return BigInteger.valueOf(k).shiftLeft(k - 3);
    }

}

Answer 3

Put $T_n = Q(n, 2)$ and taking $T_0 = 0$ by convention. Then the $T_n$ are odd when $n$ is odd and the values for even $n$ satisfy the following recursion equations:

$$ \begin{align*} T_0 &= 1 \\ T_2 &= 1 \\ T_n &= \sum_{i=1}^{n/2}T_{2(i-1)} \cdot T_{2(n/2-i)} \end{align*} $$

To see this, enumerate the vertices of the $n$-gon as $v_0, \ldots, v_{n-1}$, A solution with a connected pair $(v_i, v_j)$ with $i < j$ has to have $j -i$ odd and for $i < s < j$, $v_t$ must be connected to some $v_t$ where $i < t < j$. Thus we can connect $v_0$ to $v_1$ or $v_3$ or $v_5$ and so on. When we connect $v_0$ to $v_{2i+1}$ we get two instances of the same problem with $n$ replaced by $n'$ say, one with $n' = 2(i-1)$ and one with $n'=2(n/2-i)$. This gives:

$$T_4 = 2, T_6 = 5, T_8 = 14, T_{10} = 42$$

And (once you do the sums right $\ddot{\frown}$), these turn out as pointed out by CuddyCuttlefish to be the Catalan numbers:http://oeis.org/A000108.

Answer 4

Adapting to the changes in the question (which I do hope has stablized now and which I interpret to mean dihedral symmetry on the vertices of the polygon with three undirected possible paths in every hyperedge on three vertices) I get for $U(n,3)$ the sequence $$1, 4, 22, 201, 2244, 29096,404064,\ldots$$

This has a value of four rather than three when $n=6$ with one configuration that is missing from the diagram that appeared an hour ago. I nonetheless believe this to be the correct value. The missing configuration is the configuration consisting of two arrows with the tips pointing in opposite directions. Be sure to record this if you change the diagram now.

This was the Maple code for this computation with memoization turned off which is slower but does not consume as much memory.

with(combinat);

Q := (n,k)-> binomial(n,n/k-1)/(n/k)*(k*2^(k-3))^(n/k);

pet_autom2cyclesA :=
proc(src, aut)
local numa, numsubs;
local marks, pos, cycs, data, item, cpos, clen;

    numsubs := [seq(src[k]=k, k=1..nops(src))];
    numa := subs(numsubs, aut);

    marks := Array([seq(true, pos=1..nops(aut))]);

    cycs := []; pos := 1; data := [];

    while pos <= nops(aut) do
        if marks[pos] then
            clen := 0; item := []; cpos := pos;

            while marks[cpos] do
                marks[cpos] := false;
                item := [op(item), aut[cpos]];

                cpos := numa[cpos];
                clen := clen+1;
            od;

            cycs := [op(cycs), clen];
            data := [op(data), item];
        fi;

        pos := pos+1;
    od;

    return [data, mul(a[cycs[k]], k=1..nops(cycs))];
end;

bs_ngon_edgeconfl :=
proc(t1, t2)
    local e1, e2, c, seg;

    e1 := {op(1, t1)} union op(2, t1);
    e2 := {op(1, t2)} union op(2, t2);

    if nops(e1 union e2) <> 6 then return true fi;

    seg := [];

    for c to 3 do
        if op(1, e1) < op(c, e2) and
        op(c, e2) < op(2, e1) then
            seg := [op(seg), 1]
        elif op(2, e1) < op(c, e2) and
        op(c, e2) < op(3, e1) then
            seg := [op(seg), 2]
        else
            seg := [op(seg), 3];
        fi;
    od;

    evalb(not(seg[1] = seg[2] and seg[2] = seg[3]));
end;

bs_ngon_cycconfl :=
proc(c)
    # option remember;
    local p, q;

    for p to nops(c) do
        for q from p+1 to nops(c) do
            if bs_ngon_edgeconfl(c[p], c[q]) then
                return true;
            fi;
        od;
    od;

    return false;
end;

bs_ngon_cyc2confl :=
proc(c1, c2)
    # option remember;
    local p, q;

    for p to nops(c1) do
        for q to nops(c2) do
            if bs_ngon_edgeconfl(c1[p], c2[q]) then
                return true;
            fi;
        od;
    od;

    return false;
end;

bs_ngon_recurse :=
proc(n, cycs, pos, sofar, len)
    local res, p;

    if 3*len > n then return 0 fi;

    if pos > nops(cycs) then
        if 3*len = n then
            return 1;
        else
            return 0;
        fi;
    fi;

    res := bs_ngon_recurse(n, cycs, pos+1, sofar, len);

    for p to nops(sofar) do
        if bs_ngon_cyc2confl(cycs[sofar[p]], cycs[pos]) then
            break;
        fi;
    od;

    if p = nops(sofar) + 1 then
        res :=
        res + bs_ngon_recurse(n, cycs, pos+1,
                              [op(sofar), pos],
                              len+nops(cycs[pos]));
    fi;

    res;
end;

bs_ngon_eplanar3_paths :=
proc(n)
    option remember;
    local rot, edges_src, e, edges, autom,
    cycles, p, res;

    if type(n mod 3, positive) then return 0 fi;

    edges_src := convert(choose({seq(p, p=0..n-1)}, 3), list);

    edges := [];
    for e in edges_src do
        edges := [op(edges),
                  {e[3], {e[1], e[2]}},
                  {e[2], {e[1], e[3]}},
                  {e[1], {e[2], e[3]}}];
    od;

    res := Q(n, 3);
    # res := 0;

    for rot from 0 to n-1 do
        if rot > 0 then
            autom :=
            [seq({edges[p][1]+rot mod n,
                  {edges[p][2][1]+rot mod n,
                   edges[p][2][2]+rot mod n}},
                 p=1..nops(edges))];

            cycles := pet_autom2cyclesA(edges, autom);
            cycles :=
            select(c->not(bs_ngon_cycconfl(c)), cycles[1]);

            res := res + bs_ngon_recurse(n, cycles, 1, [], 0);
        fi;

        autom :=
        [seq({n-1-(edges[p][1]+rot) mod n,
              {n-1-(edges[p][2][1]+rot) mod n,
               n-1-(edges[p][2][2]+rot) mod n}},
             p=1..nops(edges))];

        cycles := pet_autom2cyclesA(edges, autom);
        cycles :=
        select(c->not(bs_ngon_cycconfl(c)), cycles[1]);

        res := res + bs_ngon_recurse(n, cycles, 1, [], 0);
    od;

    res/2/n;
end;

Answer 5

This is more of a "long(ish) comment" than an answer, and these are mostly my instincts speaking. But, I come bearing references!

While I won't say there's a direct connection between this and the Catalan numbers, I do suspect there is a connection, particularly involving the generalized Catalan numbers which count the ways to subdivide regular $n$-gons into $(k + 1)$-gons (Note: this isn't my field, so the variables in my description don't match what's used in the article). I don't claim there is any sort of bijection, but I imagine similar techniques could be used for both.

It is a very open problem to count the number of orbits of polygon subdivisions under the action of the dihedral group, which is what your $U(n, k)$ reminds me of. Here's a paper by Moon and Moser on orbits of triangulations of $n$-gons from several decades ago, and here are two recent theses ([1] and [2]) on orbits of more general subdivisions under the action of the dihedral group.

Again, I don't claim that these will even be related - but they are investigations of a similar nature that are essentially wide open and definitely research-level. Further, I think the polygonal dissections have a bit more structure than what you're investigating, for better or worse.

Answer 6

Remark. What follows refers to the first version of the question, which did not include dihedral symmetry.

I computed $U(n,2)$ and $U(n,3)$ (rotational symmetry) which was enough to find the relevant entries at the OEIS where we learn that this is indeed an active area of research but we also learn and I ask the reader to reflect on this, that the way we are looking at the problem here is not quite optimal and it is much better to think about it in terms of trees. I am posting my computation for the record as to how I found the correct values to query the OEIS and might return to this at some other time. I would like to stress that the OEIS entries have simple formulae and detailed references for all of this. A trip to the library is in order.

We can use Burnside to compute these. The permutation group is the action of the cyclic group on the vertices acting on the edges. We enumerate these permutations by applying the vertex permutations to an ordered list of the edges / hyperedges and factoring the result into cycles. Edges can be either on or off and we must count the number of admissible assignments that are fixed by the permutation for later averaging by the order of the group. Because the status must be constant on the cycles we turn off / turn on entire cycles at once. Cycles that contain edges that cross or share a vertex must be in the off state. The remaining cycles can be turned on or off but only as long as there are no conflicts between them (overlapping hyperedges). I used a backtracking search to count admissible cycle combinations. Finally I point out that the identity permutation is special here as it fixes all admissible assignments and hence its contribution to the Burnside average is the total number of assignments with no symmetry acting on then, i.e. $Q(n,2)$ and $Q(n,3)$ which are

$$\frac{1}{n+1}{2n\choose n}\quad\text{and}\quad \frac{1}{2n+1}{3n\choose n}.$$

This produced the following sequence for $U(n,2)$ ($n$ even) using a reasonable combination of time / space resources $$1, 1, 2, 3, 6, 14, 34, 95, 280, 854, 2694, 8714,\ldots$$

This is OEIS A002995 and that entry gives an impression of the amount of research that has gone into this sequence.

The Maple code was as follows.

CAT := n -> 1/(n+1)*binomial(2*n,n);

pet_autom2cyclesA :=
proc(src, aut)
local numa, numsubs;
local marks, pos, cycs, data, item, cpos, clen;

    numsubs := [seq(src[k]=k, k=1..nops(src))];
    numa := subs(numsubs, aut);

    marks := Array([seq(true, pos=1..nops(aut))]);

    cycs := []; pos := 1; data := [];

    while pos <= nops(aut) do
        if marks[pos] then
            clen := 0; item := []; cpos := pos;

            while marks[cpos] do
                marks[cpos] := false;
                item := [op(item), aut[cpos]];

                cpos := numa[cpos];
                clen := clen+1;
            od;

            cycs := [op(cycs), clen];
            data := [op(data), item];
        fi;

        pos := pos+1;
    od;

    return [data, mul(a[cycs[k]], k=1..nops(cycs))];
end;

bs_ngon_edgeconfl :=
proc(e1, e2)
    local c;

    if nops(e1 union e2) <> 4 then return true fi;

    c := 0;

    if op(1, e1) < op(1, e2) and
    op(1, e2) < op(2, e1) then
        c := c+1;
    fi;

    if op(1, e1) < op(2, e2) and
    op(2, e2) < op(2, e1) then
        c := c+1;
    fi;

    evalb(c = 1);
end;

bs_ngon_cycconfl :=
proc(c)
    option remember;
    local p, q;

    for p to nops(c) do
        for q from p+1 to nops(c) do
            if bs_ngon_edgeconfl(c[p], c[q]) then
                return true;
            fi;
        od;
    od;

    return false;
end;

bs_ngon_cyc2confl :=
proc(c1, c2)
    option remember;
    local p, q;

    for p to nops(c1) do
        for q to nops(c2) do
            if bs_ngon_edgeconfl(c1[p], c2[q]) then
                return true;
            fi;
        od;
    od;

    return false;
end;

bs_ngon_recurse :=
proc(n, cycs, pos, sofar, len)
    local res, p;

    if 2*len > n then return 0 fi;

    if pos > nops(cycs) then
        if 2*len = n then
            return 1
        else
            return 0;
        fi;
    fi;

    res := bs_ngon_recurse(n, cycs, pos+1, sofar, len);

    for p to nops(sofar) do
        if bs_ngon_cyc2confl(cycs[sofar[p]], cycs[pos]) then
            break;
        fi;
    od;

    if p = nops(sofar) + 1 then
        res :=
        res + bs_ngon_recurse(n, cycs, pos+1,
                              [op(sofar), pos],
                              len+nops(cycs[pos]));
    fi;

    res;
end;

bs_ngon_eplanar :=
proc(n)
    option remember;
    local rot, edges, autom, cycles, p, q, res;

    if type(n, odd) then return 0 fi;

    edges := [seq(seq({p,q}, q=p+1..n-1), p=0..n-1)];
    res := CAT(n/2);

    for rot to n-1 do
        autom :=
        [seq({edges[p][1]+rot mod n, edges[p][2]+rot mod n},
             p=1..nops(edges))];

        cycles := pet_autom2cyclesA(edges, autom);
        cycles :=
        select(c->not(bs_ngon_cycconfl(c)), cycles[1]);

        res := res + bs_ngon_recurse(n, cycles, 1, [], 0);
    od;

    res/n;
end;

For $U(n,3)$ we obtain the following sequence ($n$ a multiple of three), again using a reasonable combination of time / space resources $$1, 1, 2, 7, 19, 86, 372, 1825, 9143,\ldots$$

This is OEIS A054423, once more an entry with considerable activity.

This was the Maple code.

with(combinat);

CAT3 := n -> 1/(2*n+1)*binomial(3*n,n);

pet_autom2cyclesA :=
proc(src, aut)
local numa, numsubs;
local marks, pos, cycs, data, item, cpos, clen;

    numsubs := [seq(src[k]=k, k=1..nops(src))];
    numa := subs(numsubs, aut);

    marks := Array([seq(true, pos=1..nops(aut))]);

    cycs := []; pos := 1; data := [];

    while pos <= nops(aut) do
        if marks[pos] then
            clen := 0; item := []; cpos := pos;

            while marks[cpos] do
                marks[cpos] := false;
                item := [op(item), aut[cpos]];

                cpos := numa[cpos];
                clen := clen+1;
            od;

            cycs := [op(cycs), clen];
            data := [op(data), item];
        fi;

        pos := pos+1;
    od;

    return [data, mul(a[cycs[k]], k=1..nops(cycs))];
end;

bs_ngon_edgeconfl :=
proc(e1, e2)
    local c, seg;

    if nops(e1 union e2) <> 6 then return true fi;

    seg := [];

    for c to 3 do
        if op(1, e1) < op(c, e2) and
        op(c, e2) < op(2, e1) then
            seg := [op(seg), 1]
        elif op(2, e1) < op(c, e2) and
        op(c, e2) < op(3, e1) then
            seg := [op(seg), 2]
        else
            seg := [op(seg), 3];
        fi;
    od;

    evalb(not(seg[1] = seg[2] and seg[2] = seg[3]));
end;

bs_ngon_cycconfl :=
proc(c)
    option remember;
    local p, q;

    for p to nops(c) do
        for q from p+1 to nops(c) do
            if bs_ngon_edgeconfl(c[p], c[q]) then
                return true;
            fi;
        od;
    od;

    return false;
end;

bs_ngon_cyc2confl :=
proc(c1, c2)
    option remember;
    local p, q;

    for p to nops(c1) do
        for q to nops(c2) do
            if bs_ngon_edgeconfl(c1[p], c2[q]) then
                return true;
            fi;
        od;
    od;

    return false;
end;

bs_ngon_recurse :=
proc(n, cycs, pos, sofar, len)
    local res, p;

    if 3*len > n then return 0 fi;

    if pos > nops(cycs) then
        if 3*len = n then
            return 1
        else
            return 0;
        fi;
    fi;

    res := bs_ngon_recurse(n, cycs, pos+1, sofar, len);

    for p to nops(sofar) do
        if bs_ngon_cyc2confl(cycs[sofar[p]], cycs[pos]) then
            break;
        fi;
    od;

    if p = nops(sofar) + 1 then
        res :=
        res + bs_ngon_recurse(n, cycs, pos+1,
                              [op(sofar), pos],
                              len+nops(cycs[pos]));
    fi;

    res;
end;

bs_ngon_eplanar3 :=
proc(n)
    option remember;
    local rot, edges, autom, cycles, p, res;

    if type(n mod 3, positive) then return 0 fi;

    edges := convert(choose({seq(p, p=0..n-1)}, 3), list);
    res := CAT3(n/3);

    for rot to n-1 do
        autom :=
        [seq({edges[p][1]+rot mod n, 
              edges[p][2]+rot mod n,
              edges[p][3]+rot mod n},
             p=1..nops(edges))];

        cycles := pet_autom2cyclesA(edges, autom);
        cycles :=
        select(c->not(bs_ngon_cycconfl(c)), cycles[1]);

        res := res + bs_ngon_recurse(n, cycles, 1, [], 0);
    od;

    res/n;
end;

Addendum. As per the comments I was definitely counting polygons and not paths. However this appears to be a simple matter of adding in factor of $3^\mathrm{len}$ to the backtracking search engine when a decomposition into polygons is found. This produces the sequence $$3, 9, 54, 567, 4617, 62694, 813564, 11973825,\ldots$$ which does not have an OEIS entry yet. The Maple code here is the same as before except for the following changes:

Q := (n,k)-> binomial(n,n/k-1)/(n/k)*(k*2^(k-3))^(n/k);

bs_ngon_recurse :=
proc(n, cycs, pos, sofar, len)
    local res, p;

    if 3*len > n then return 0 fi;

    if pos > nops(cycs) then
        if 3*len = n then
            return 3^len
        else
            return 0;
        fi;
    fi;

    res := bs_ngon_recurse(n, cycs, pos+1, sofar, len);

    for p to nops(sofar) do
        if bs_ngon_cyc2confl(cycs[sofar[p]], cycs[pos]) then
            break;
        fi;
    od;

    if p = nops(sofar) + 1 then
        res :=
        res + bs_ngon_recurse(n, cycs, pos+1,
                              [op(sofar), pos],
                              len+nops(cycs[pos]));
    fi;

    res;
end;

bs_ngon_eplanar3_paths :=
proc(n)
    option remember;
    local rot, edges, autom, cycles, p, res;

    if type(n mod 3, positive) then return 0 fi;

    edges := convert(choose({seq(p, p=0..n-1)}, 3), list);
    res := Q(n, 3);

    for rot to n-1 do
        autom :=
        [seq({edges[p][1]+rot mod n,
              edges[p][2]+rot mod n,
              edges[p][3]+rot mod n},
             p=1..nops(edges))];

        cycles := pet_autom2cyclesA(edges, autom);
        cycles :=
        select(c->not(bs_ngon_cycconfl(c)), cycles[1]);

        res := res + bs_ngon_recurse(n, cycles, 1, [], 0);
    od;

    res/n;
end;

Addendum II. Using the same algorithm as above (which I can post if desired) I get the following values for $U(n,4):$ $$8, 64, 1536, 45056, 1703936, 80478208,\ldots$$ which I hope can serve to verify the correctness of a better algorithm that might appear in this discussion.

Answer 7

By introducing parallelism into the algorithm for $U(n,3)$ using the Maple task parallel programming framework I was able to compute another value from the sequence, which now reads $$1, 4, 22, 201, 2244, 29096, 404064, 5915838,\ldots$$ It is hoped that these values can serve to verify a more sophisticated algorithm if and when it appears. Peak usage was 18 processors at 2GHz with about 60 minutes computation time and max memory allocation 4.6GB.

This was the Maple code.

with(combinat);

Q := (n,k)-> binomial(n,n/k-1)/(n/k)*(k*2^(k-3))^(n/k);

pet_autom2cyclesA :=
proc(src, aut)
local numa, numsubs;
local marks, pos, cycs, data, item, cpos, clen;

    numsubs := [seq(src[k]=k, k=1..nops(src))];
    numa := subs(numsubs, aut);

    marks := Array([seq(true, pos=1..nops(aut))]);

    cycs := []; pos := 1; data := [];

    while pos <= nops(aut) do
        if marks[pos] then
            clen := 0; item := []; cpos := pos;

            while marks[cpos] do
                marks[cpos] := false;
                item := [op(item), aut[cpos]];

                cpos := numa[cpos];
                clen := clen+1;
            od;

            cycs := [op(cycs), clen];
            data := [op(data), item];
        fi;

        pos := pos+1;
    od;

    return [data, mul(a[cycs[k]], k=1..nops(cycs))];
end;

bs_ngon_edgeconfl :=
proc(t1, t2)
    local e1, e2, c, seg;

    e1 := {op(1, t1)} union op(2, t1);
    e2 := {op(1, t2)} union op(2, t2);

    if nops(e1 union e2) <> 6 then return true fi;

    seg := [];

    for c to 3 do
        if op(1, e1) < op(c, e2) and
        op(c, e2) < op(2, e1) then
            seg := [op(seg), 1]
        elif op(2, e1) < op(c, e2) and
        op(c, e2) < op(3, e1) then
            seg := [op(seg), 2]
        else
            seg := [op(seg), 3];
        fi;
    od;

    evalb(not(seg[1] = seg[2] and seg[2] = seg[3]));
end;

bs_ngon_cycconfl :=
proc(c)
    option remember;
    local p, q;

    for p to nops(c) do
        for q from p+1 to nops(c) do
            if bs_ngon_edgeconfl(c[p], c[q]) then
                return true;
            fi;
        od;
    od;

    return false;
end;

bs_ngon_cyc2confl :=
proc(c1, c2)
    option remember;
    local p, q;

    for p to nops(c1) do
        for q to nops(c2) do
            if bs_ngon_edgeconfl(c1[p], c2[q]) then
                return true;
            fi;
        od;
    od;

    return false;
end;

bs_ngon_admissible :=
proc(n, cycs)
    local adms, item, nxtgen, cind, pos, res;

    if nops(cycs) = 0 then return 0 fi;

    adms := [ [1] ];

    for cind from 2 to nops(cycs) do
        nxtgen := [ [cind] ];

        for item in adms do
            for pos to nops(item) do
                if bs_ngon_cyc2confl
                (cycs[cind], cycs[item[pos]]) then
                    break;
                fi;
            od;

            if pos = nops(item) + 1 then
                nxtgen := [op(nxtgen), [op(item), cind]];
            fi;
        od;

        adms := [op(adms), 
                 seq(nxtgen[pos], pos=1..nops(nxtgen))];
    od;

    res := 0;

    for item in adms do
        if 3*add(nops(cycs[pos]), pos in item) = n then
            res := res + 1;
        fi;
    od;

    res;
end;

bs_ngon_eplanar3_paths_task :=
proc(n)
    option remember;
    local rot, edges_src, e, edges, autom, cargs,
    cycles, p;

    if type(n mod 3, positive) then return 0 fi;

    edges_src := convert(choose({seq(p, p=0..n-1)}, 3), list);

    edges := [];
    for e in edges_src do
        edges := [op(edges),
                  {e[3], {e[1], e[2]}},
                  {e[2], {e[1], e[3]}},
                  {e[1], {e[2], e[3]}}];
    od;

    cargs := [];

    for rot from 0 to n-1 do
        if rot > 0 then
            autom :=
            [seq({edges[p][1]+rot mod n,
                  {edges[p][2][1]+rot mod n,
                   edges[p][2][2]+rot mod n}},
                 p=1..nops(edges))];

            cycles := pet_autom2cyclesA(edges, autom);
            cycles :=
            select(c->not(bs_ngon_cycconfl(c)), cycles[1]);

            cargs := [op(cargs), [n, cycles]];
        fi;

        autom :=
        [seq({n-1-(edges[p][1]+rot) mod n,
              {n-1-(edges[p][2][1]+rot) mod n,
               n-1-(edges[p][2][2]+rot) mod n}},
             p=1..nops(edges))];

        cycles := pet_autom2cyclesA(edges, autom);
        cycles :=
        select(c->not(bs_ngon_cycconfl(c)), cycles[1]);

        cargs := [op(cargs), [n, cycles]];
    od;

    Threads:-Task:-Continue
    (`+`, Tasks = [bs_ngon_admissible, seq(p, p in cargs)]);
end;

bs_ngon_eplanar3_paths :=
proc(n)
    option remember;
    local res;

    res := Q(n, 3)+
    Threads:-Task:-Start(bs_ngon_eplanar3_paths_task, n);

    res/2/n;
end;

Addendum Mon Jun 1 22:05:48 CEST 2015. Here is a simple Maple routine that computes the first three nonzero values of $U(n,3)$ by total enumeration. They turn out to be $1, 4, 22$, which confirms the results from the application of Burnside's lemma. This seems to be about the limit where brute force is concerned.

with(combinat);

bs_ngon_edgeconfl :=
proc(t1, t2)
    local e1, e2, c, seg;

    e1 := {op(1, t1)} union op(2, t1);
    e2 := {op(1, t2)} union op(2, t2);

    if nops(e1 union e2) <> 6 then return true fi;

    seg := [];

    for c to 3 do
        if op(1, e1) < op(c, e2) and
        op(c, e2) < op(2, e1) then
            seg := [op(seg), 1]
        elif op(2, e1) < op(c, e2) and
        op(c, e2) < op(3, e1) then
            seg := [op(seg), 2]
        else
            seg := [op(seg), 3];
        fi;
    od;

    evalb(not(seg[1] = seg[2] and seg[2] = seg[3]));
end;


bs_ngon_eplanar3_paths :=
proc(n)
    option remember;
    local rot, edges_src, e, f, p, edges, res, selc, sel,
    item, admit, autom, sl;

    if type(n mod 3, positive) then return 0 fi;

    edges_src := choose([seq(p, p=0..n-1)], 3);

    edges := {};
    for e in edges_src do
        edges := {op(edges),
                  {e[3], {e[1], e[2]}},
                  {e[2], {e[1], e[3]}},
                  {e[1], {e[2], e[3]}}};
    od;

    sl := [];

    for rot from 0 to n-1 do
        sl := [op(sl), [seq(p=(p+rot) mod n, p=0..n-1)]];
        sl := [op(sl), [seq(p=(n-1-(p+rot)) mod n, p=0..n-1)]];
    od;

    res := {};

    selc := firstcomb(nops(edges), n/3);

    while type(selc, set) do
        sel := {seq(edges[selc[p]], p=1..n/3)};

        admit := true;

        for e to nops(sel) do
            for f from e+1 to nops(sel) do
                if bs_ngon_edgeconfl(sel[e], sel[f]) then
                    admit := false;
                fi;
            od;
        od;

        if admit then
            item := {};

            for p in sl do
                item := item union {subs(p, sel)};
            od;

            res := res union {item};
        fi;

        selc := nextcomb(selc, nops(edges));
    od;

    nops(res);
end;

Answer 8

Sequences in Oeis related to this are those titled "noncrossing path sets". A302828 gives a table of $U(n,k)$ with column 3 and 4 being A303330 and A303867. Other sequences have been added for the cases of counting only distinct solutions up to rotation and also for mixed path lengths.

Noncrossing path sets are a subclass of noncrossing graphs. Other subclasses include noncrossing trees, forests and partitions and also dissections of a polygon by nonintersecting diagonals. There is much literature on some of these.

The method of solution requires the use of Burnsides' lemma. Firstly it is necessary to look at the number of symmetrical configurations of a single path. Rotation: A path on an odd number of nodes cannot have rotational symmetry, and for even $k$ the number of paths with $180$ degree rotational symmetry is $2^{k/2-1}$. Reflection: For odd $k$, there are $2^{(k-3)/2}$ paths that are symmetrical and for even $k$, there are $2^{k/2-1}$ with the line symmetry drawn between the two central nodes. There is also a special case when $k=2$ of a line of symmetry connecting the two nodes.

It is easier to work with generating functions. In particular, if $g$ is the generating function for a class of combinatoric object (in this case, noncrossing path sets), then $g^2$, $g^3$, etc will give the generating function for an ordered pair, triple etc of those objects. Also $1/(1-g)$ is the generating function for a sequence of zero or more of such objects. Differentiating is a trick to multiply the $n^{th}$ term by $n$, and integration is a similar trick for dividing the $n^{th}$ term by $n$. A good introductory text on the use of generating functions for counting is Chapter 1 of Analytic Combinatorics by Flajolet and Sedgewick which available for free download.

The generating function for $Q$ is given by $1 + \text{serreverse}( x/(k*2^{k-3}*(1 + x)^k)$ where serreverse is series reversion. The $1$ at the beginning is important to also provide an option for an empty set. (when computing $g^r$ we typically want to allow some of the parts to be empty). For the case of $k=3$ this expands to $1 + 3*x + 27*x^2 + 324*x^3 + 4455*x^4 + 66339*x^5 ...$.

The rest is left as an exercise for the reader. (sorry - it would take many illustrations to explain everything in a satisfactory way). Reference material: A similar problem is that of polygon dissection (some details differ). 1. F. Harary, E. M. Palmer and R. C. Read, On the cell-growth problem for arbitrary polygons, Discr. Math. 11 (1975), 371-389. 2. E. Krasko, A. Omelchenko, Brown's Theorem and its Application for Enumeration of Dissections and Planar Trees, The Electronic Journal of Combinatorics, 22 (2015), #P1.17. If those are a bit heavy, there is also a short note https://oeis.org/A175954/a175954.txt that deals with the case where paths cover either 1 or two nodes. (this note has a couple of egregious errors, but it covers the considerations are almost identical to those required for paths of longer length).